Chapter 5
Advanced Topics in Single-Variable Calculus and an Introduction to Multivariable Calculus
By Boundless
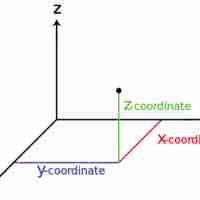
The three-dimensional coordinate system expresses a point in space with three parameters, often length, width and depth (

Vectors are needed in order to describe a plane and can give the direction of all dimensions in one vector equation.
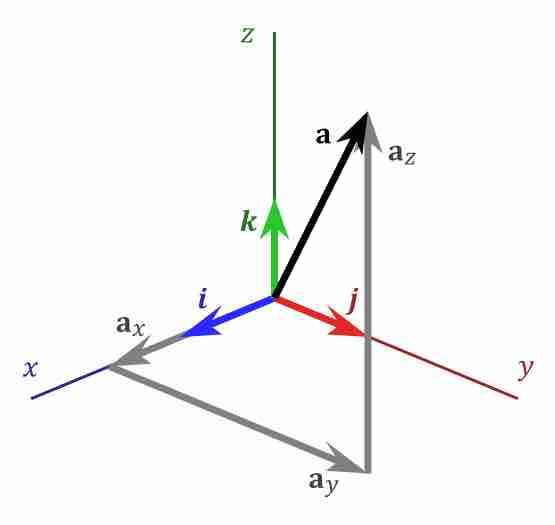
A Euclidean vector is a geometric object that has magnitude (i.e. length) and direction.
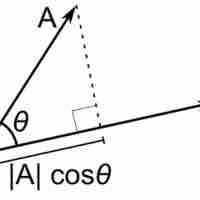
The dot product takes two vectors of the same dimension and returns a single value.
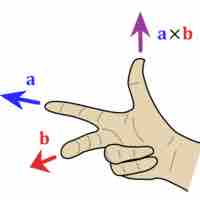
The cross product of two vectors is a vector which is perpendicular to both of the original vectors.
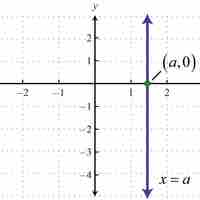
A line is a vector which connects two points on a plane and the direction and magnitude of a line determine the plane on which it lies.
A quadric surface is any
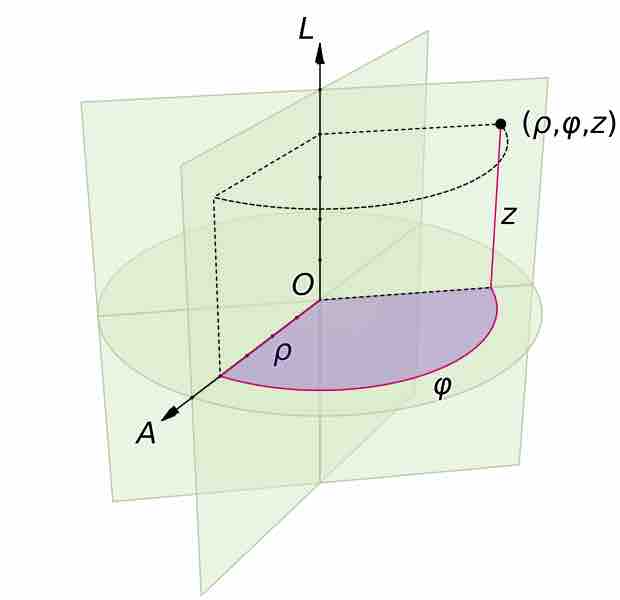
Cylindrical and spherical coordinates are useful when describing objects or phenomena with specific symmetries.
A surface is a two-dimensional, topological manifold.
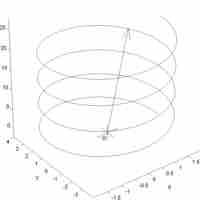
A vector function covers a set of multidimensional vectors at the intersection of the domains of
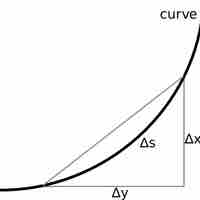
Arc length and speed are, respectively, a function of position and its derivative with respect to time.
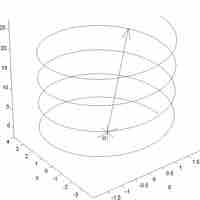
A vector function is a function that can behave as a group of individual vectors and can perform differential and integral operations.

The curvature of an object is the degree to which it deviates from being flat and can be found using arc length.
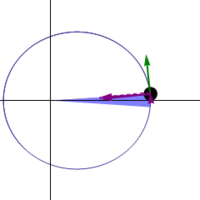
Kepler explained that the planets move in an ellipse around the Sun, which is at one of the two foci of the ellipse.
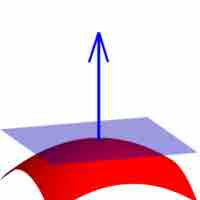
A vector is normal to another vector if the intersection of the two form a 90-degree angle at the tangent point.
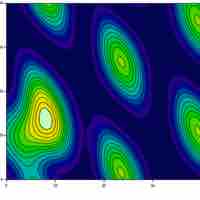
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable.
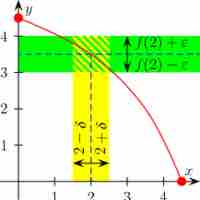
A study of limits and continuity in multivariable calculus yields counter-intuitive results not demonstrated by single-variable functions.
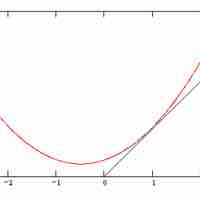
A partial derivative of a function of several variables is its derivative with respect to a single variable, with the others held constant.
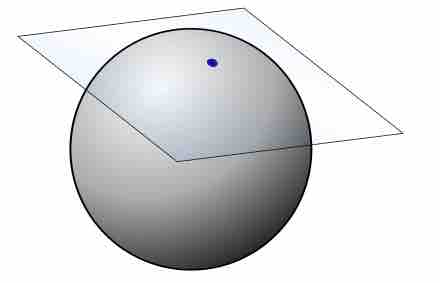
The tangent plane to a surface at a given point is the plane that "just touches" the surface at that point.
For a function
The directional derivative represents the instantaneous rate of change of the function, moving through

The second partial derivative test is a method used to determine whether a critical point is a local minimum, maximum, or saddle point.

The method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints.

To solve an optimization problem, formulate the function
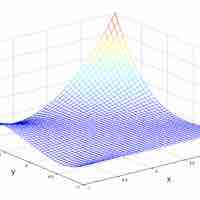
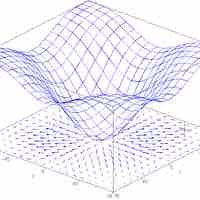
Finding extrema can be a challenge with regard to multivariable functions, requiring careful calculation.

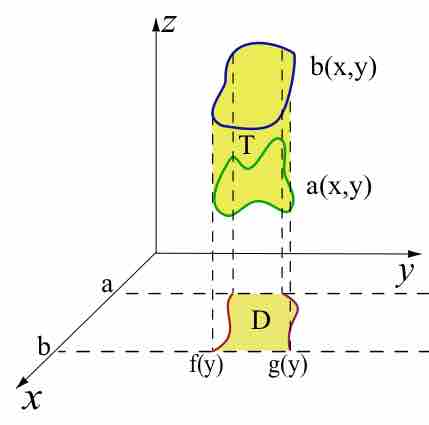
For a rectangular region

An iterated integral is the result of applying integrals to a function of more than one variable.
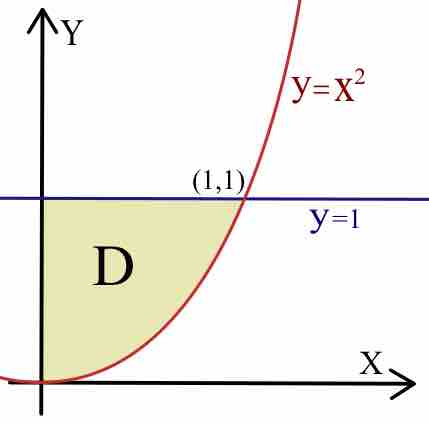
Double integrals can be evaluated over the integral domain of any general shape.
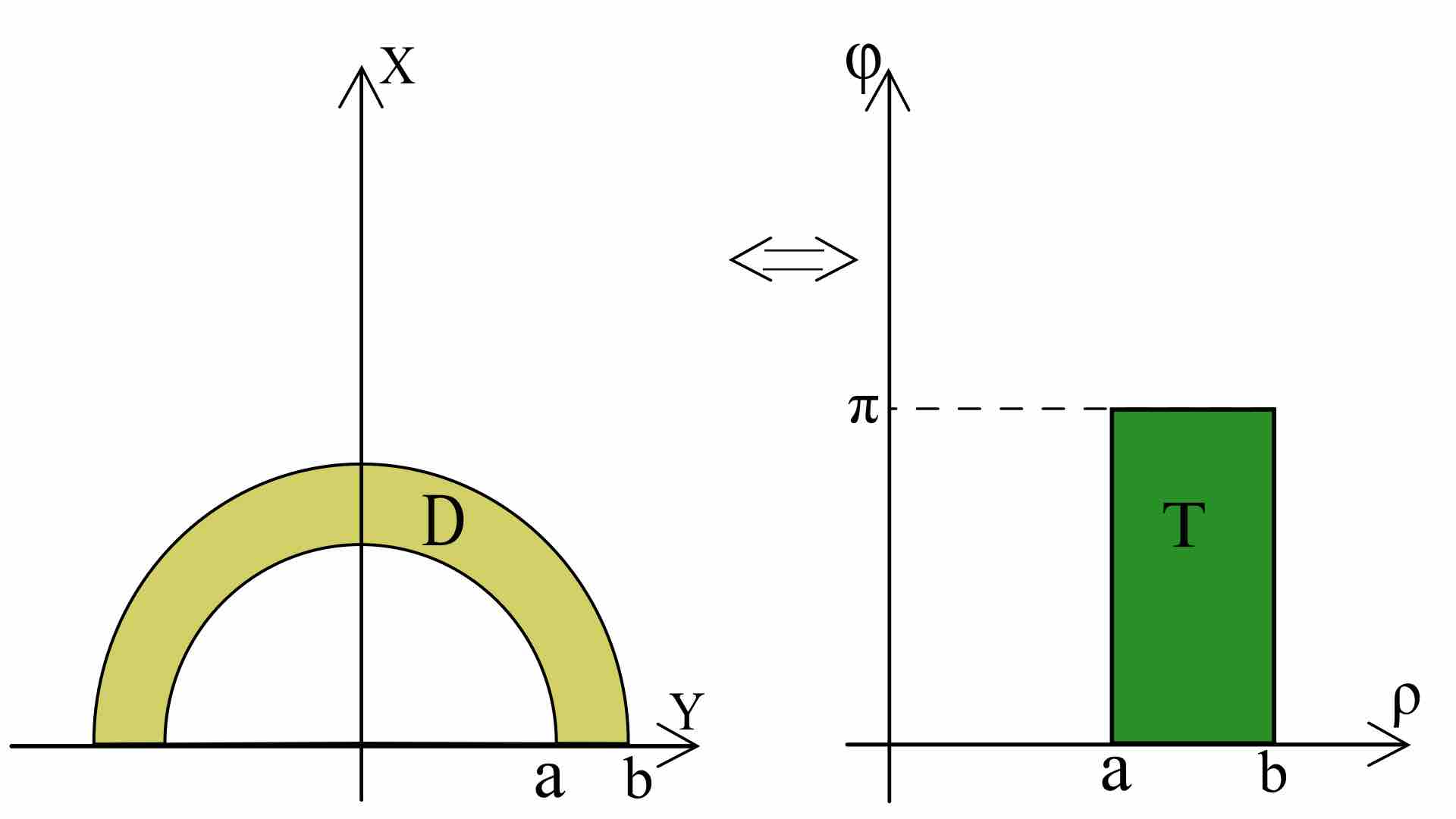
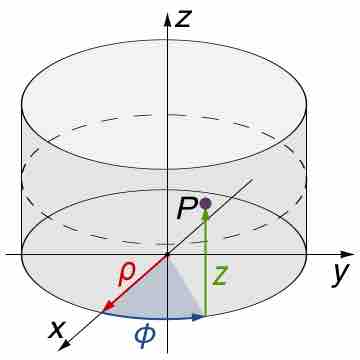
When domain has a cylindrical symmetry and the function has several specific characteristics, apply the transformation to polar coordinates.
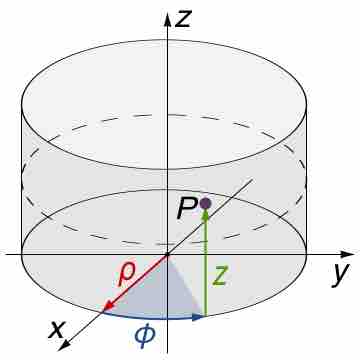
When the function to be integrated has a cylindrical symmetry, it is sensible to integrate using cylindrical coordinates.
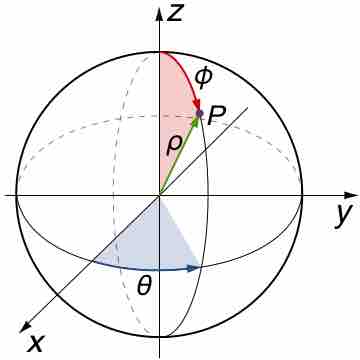
When the function to be integrated has a spherical symmetry, change the variables into spherical coordinates and then perform integration.
For
One makes a change of variables to rewrite the integral in a more "comfortable" region, which can be described in simpler formulae.
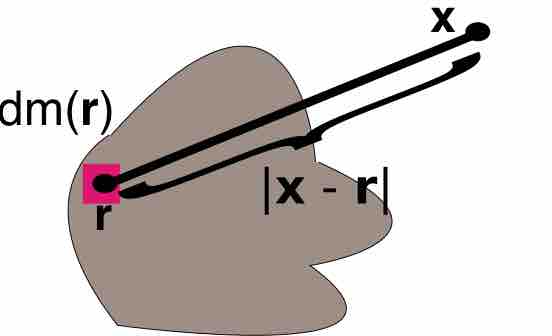
Multiple integrals are used in many applications in physics and engineering.
The center of mass for a rigid body can be expressed as a triple integral.

A vector field is an assignment of a vector to each point in a subset of Euclidean space.
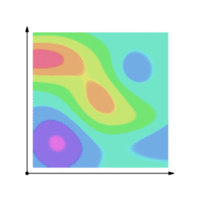
A conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential.
A line integral is an integral where the function to be integrated is evaluated along a curve.
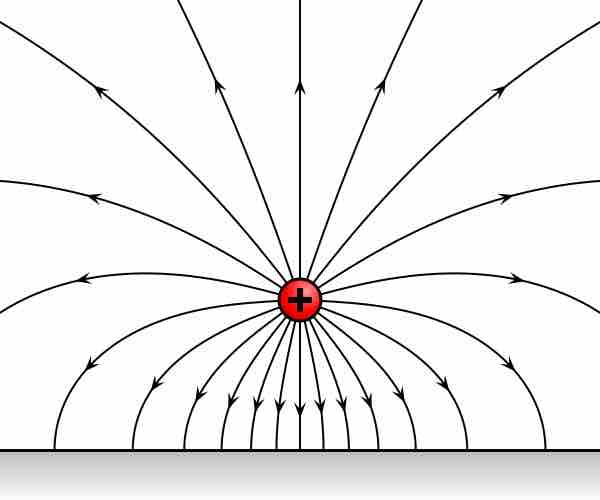
Gradient theorem says that a line integral through a gradient field can be evaluated from the field values at the endpoints of the curve.
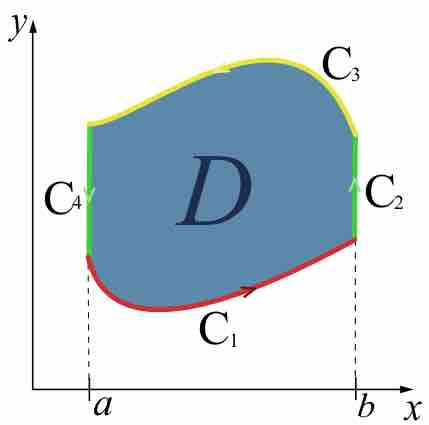
Green's theorem gives relationship between a line integral around closed curve

The four most important differential operators are gradient, curl, divergence, and Laplacian.
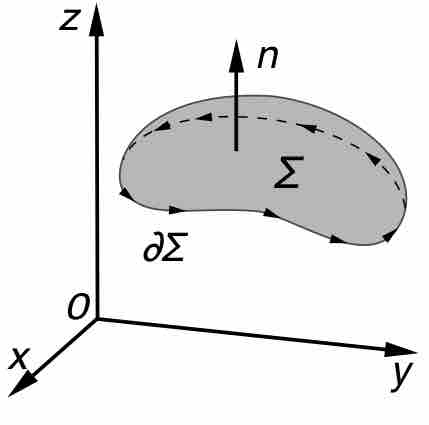
A parametric surface is a surface in the Euclidean space
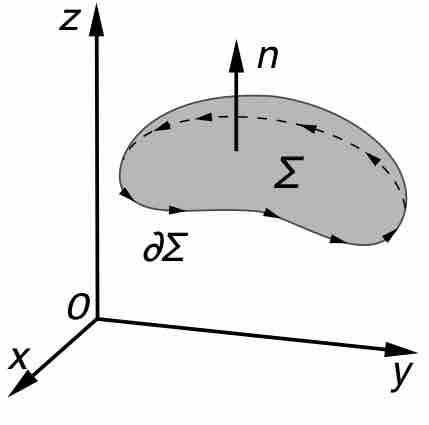
The surface integral of vector fields can be defined component-wise according to the definition of the surface integral of a scalar field.
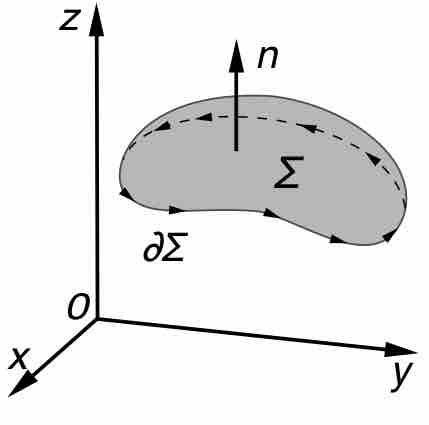
Stokes' theorem relates the integral of the curl of a vector field over a surface to the line integral of the field around the boundary.
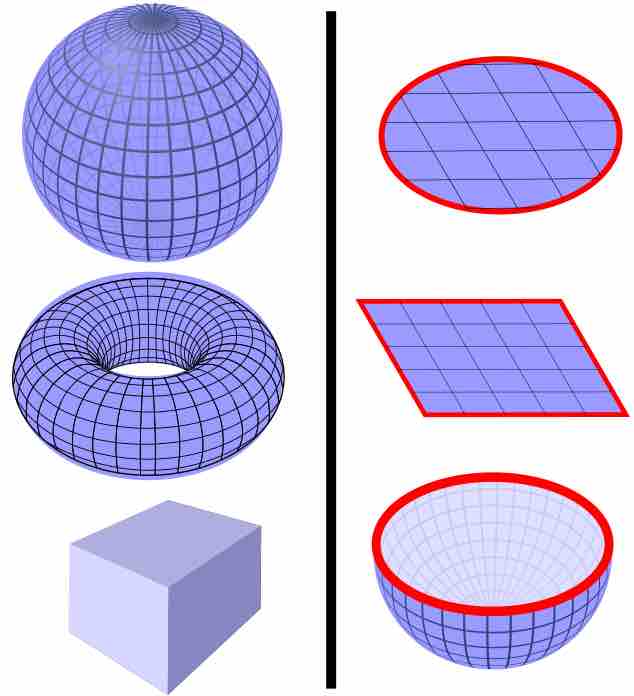
The divergence theorem relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.
A second-order linear differential equation has the form
Nonhomogeneous second-order linear equation are of the the form:
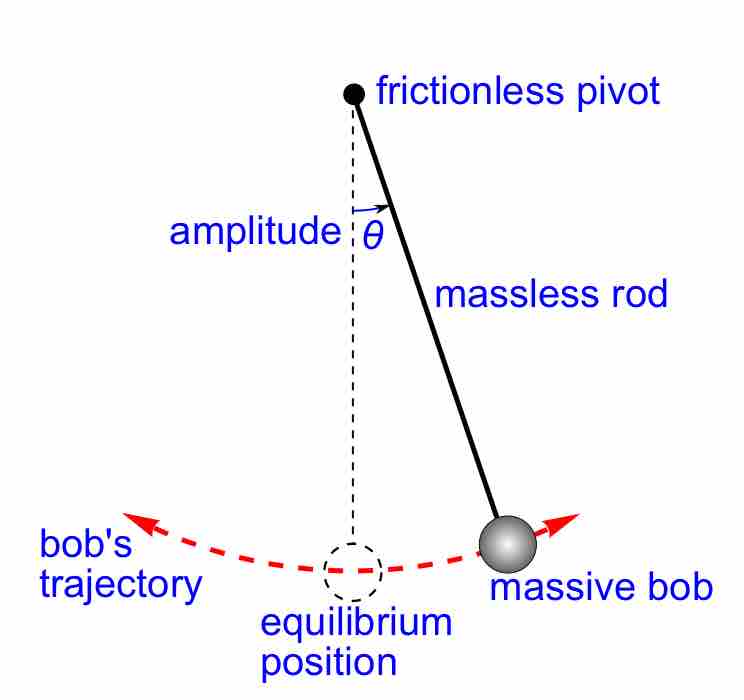
A second-order linear differential equation can be commonly found in physics, economics, and engineering.
The power series method is used to seek a power series solution to certain differential equations.