Vectors in the Plane
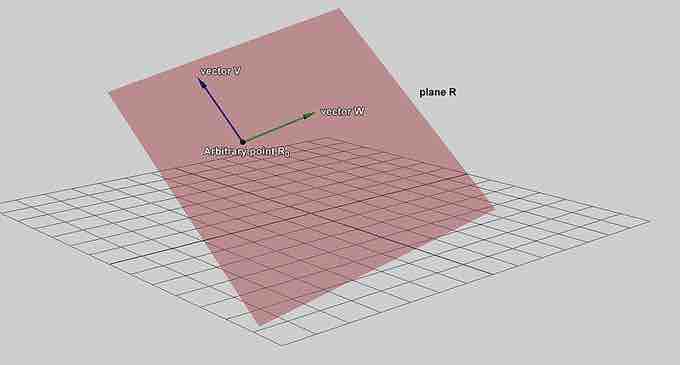
Planes in a three dimensional space can be described mathematically using a point in the plane and a vector to indicate its "inclination".
Normal Vector to a Plane
This plane may be described parametrically as the set of all points of the form
General form of the equation of the plane
In order to find the equation of the plane, consider the following: Let
The plane determined by this point and vector consists of those points
We can expand this equation in terms of its components to give:
which we call the point-normal equation of the plane and is the general equation we use to describe the plane.