A Euclidean vector (sometimes called a geometric or spatial vector, or—as here—simply a vector) is a geometric object that has magnitude (or length) and direction and can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a line segment with a definite direction, or graphically as an arrow, connecting an initial point
Vectors play an important role in physics: velocity and acceleration of a moving object and forces acting on it are all described by vectors. Many other physical quantities can be usefully thought of as vectors. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.
In the Cartesian coordinate system, a vector can be represented by identifying the coordinates of its initial and terminal point. For instance, in three dimensions, the points
Typically in Cartesian coordinates, one considers primarily bound vectors. A bound vector is determined by the coordinates of the terminal point, its initial point always having the coordinates of the origin
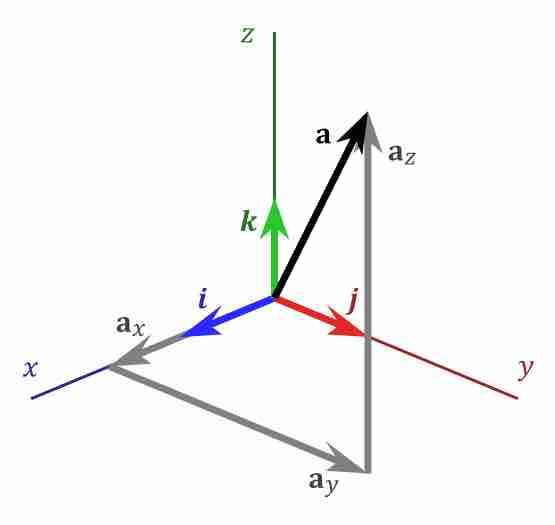
Vector in 3D Space
A vector in the 3D Cartesian space, showing the position of a point