The Dot Product

The Dot Product

The dot product takes two vectors and returns a single value. The dot product can only be taken from two vectors of the same dimension. The dot product is the sum of the product of the corresponding parameters. Geometrically, the dot product is the product of the magnitudes of two vectors and the cosine of the angle between them. This is different from the cross product, which gives an answer in vector form.

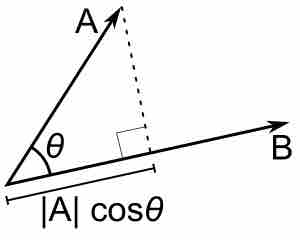
Dot Product

When finding the dot product geometrically, you need the magnitudes of the vectors and the angle between them.

There are two representations of the dot product:

1. $\vec a \cdot \vec b = a_1b_1 + a_2b_2 + a_3b_3$
2. $\vec A \cdot \vec B = | A | |B | \cos \theta$

Properties

Some of the properties of the dot product are

• The dot product is a commutative property, which means that the order of the terms does not change the outcome: $\vec a \cdot \vec b = \vec b \cdot \vec a$
• The dot product is a distributive property: $\vec a \cdot ( \vec b+ \vec c ) = \vec a \cdot \vec b + \vec a \cdot \vec c$
• If two vectors are normal (perpendicular) to each other, their dot product will be equal to zero: $\vec a \cdot \vec b = 0$

Example

Find the dot product of the two vectors $\vec{Q}(5,2,8)$ and $\vec{R}(6,-2,9)$:

$\vec Q \cdot \vec R = Q_1 R_1 + Q_2 R_2 + Q_3 R_3 \\ = 5 \cdot 6 + 2 \cdot ( -2) + 8 \cdot 9 \\ = 98$