The Cross Product

The cross product is a binary operation of two three-dimensional vectors. The result is a vector which is perpendicular to both of the original vectors. Because it is perpendicular to both original vectors, the resulting vector is normal to the plane of the original vectors.

If the two original vectors are parallel to each other, the cross product will be zero.

The cross product is denoted as $a \times b = c$.

The direction of vector $c$ can be found by using the right hand rule. 

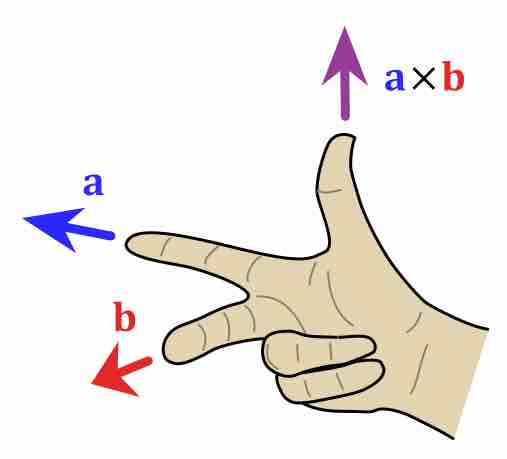
The Right Hand Rule

If you use the rules shown in the figure, your thumb will be pointing in the direction of vector $c$, the cross product of the vectors.

The magnitude of vector $c$ is equal to the area of the parallelogram made by the two original vectors.

The cross product is different from the dot product because the answer is in vector form in the same number of dimensions as the original two vectors, where the dot product is given in the form of a single quantity in one dimension.

The cross product can be found both algebraically and geometrically.

The geometric method of finding the cross product uses the magnitudes of the vectors and the sine of the angle between them:

$a \times b = \left| a \right| \left| b \right| \sin \theta$

The algebraic method of finding the cross product of two vectors involves inputting the vector information into matrices and manipulating them:

$=\left[ {\begin{array}{cc} a_2 & a_3 \\ b_2 & b_3 \\ \end{array} } \right]i - \left[ {\begin{array}{cc} a_1 & a_3 \\ b_1 & b_3 \\ \end{array} } \right]j + \left[ {\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \\ \end{array} } \right]k\\ =\left[ {\begin{array}{cc} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{array} } \right]\\ $

The manipulated matrices form the following equations:

$=< a_2b_3 - a_3b_2 , a_3b_1 - a_1b_3 , a_1b_2 - a_2b_1 >$