For
Notice that, by convention, the triple integral has three integral signs (and a double integral has two integral signs); this is a notational convention which is convenient when computing a multiple integral as an iterated integral.
We have seen that double integrals can be evaluated over regions with a general shape. The extension of those formulae to triple integrals should be apparent. If
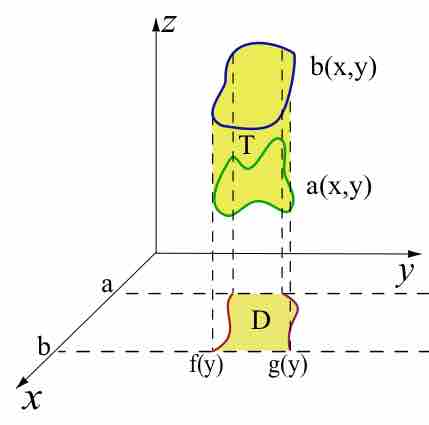
Graphical Representation of a Triple Integral
Example of domain in
Example 1
The volume of the parallelepiped of sides 4 by 6 by 5 may be obtained in two ways:
- By calculating the double integral of the function
$f(x, y) = 5$ over the region$D$ in the$xy$ -plane which is the base of the parallelepiped:$\iint_D 5 \ dx\, dy$ - By calculating the triple integral of the constant function 1 over the parallelepiped itself:
$\iiint_\mathrm{parallelepiped} 1 \, dx\, dy\, dz$
Example 2
Integrate
Looking at the domain, it seems convenient to adopt the passage in spherical coordinates; in fact, the intervals of the variables that delimit the new
For the function, we get:
Therefore: