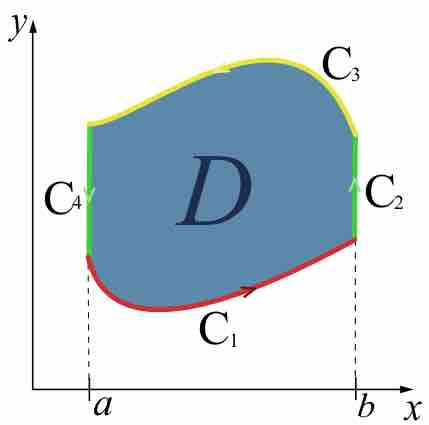
Green's Theorem

Green's theorem gives the relationship between a line integral around a simple closed curve $C$ and a double integral over the plane region $D$ bounded by $C$.

Let $C$ be a positively oriented, piecewise smooth, simple closed curve in a plane, and let $D$ be the region bounded by $C$. If $L$ and $M$ are functions of $(x,y)$ defined on an open region containing $D$ and have continuous partial derivatives there, then:

$\displaystyle{\oint_{C} (L\, \mathrm{d}x + M\, \mathrm{d}y) = \iint_{D} \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\, \mathrm{d}x\, \mathrm{d}y}$

where the path of integration along $C$ is counterclockwise.

In physics, Green's theorem is mostly used to solve two-dimensional flow integrals, stating that the sum of fluid outflows at any point inside a volume is equal to the total outflow summed about an enclosing area. In plane geometry and area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter.

Green's theorem is a special case of the Kelvin–Stokes theorem, when applied to a region in the $xy$-plane. Considering only two-dimensional vector fields, Green's theorem is equivalent to the two-dimensional version of the divergence theorem.

Computing area by line integral

$D$ is a simple region with its boundary consisting of the curves $C_1$, $C_2$, $C_3$, $C_4$. Green's theorem can be used to compute area by line integral. The area is given by $A = \iint_{D}\mathrm{d}A$. Provided we choose $L$ and $M$ such that: $\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y} = 1$, then the area is given by $A=\oint_{C} x$. Possible formulas for the area of $D$ include: $A=\oint_{C} xdy$, $A = -\oint_{C} ydx$, and $A = \frac{1}{2}\oint_{C} (xdy - ydx)$.