Fundamental Theorem for Line Integrals

The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve.

Let $\varphi : U \subseteq \mathbb{R}^n \to \mathbb{R}$. This holds that:

$\displaystyle{\varphi\left(\mathbf{q}\right)-\varphi\left(\mathbf{p}\right) = \int_{\gamma[\mathbf{p},\,\mathbf{q}]} \nabla\varphi(\mathbf{r})\cdot d\mathbf{r}}$

It is a generalization of the fundamental theorem of calculus to any curve in a plane or space (generally $n$-dimensional) rather than just the real line.

The gradient theorem implies that line integrals through irrotational vector fields are path-independent. In physics this theorem is one of the ways of defining a "conservative force." By placing $\varphi$ as potential, $\nabla$ is a conservative field. Work done by conservative forces does not depend on the path followed by the object, but only the end points, as the above equation shows.

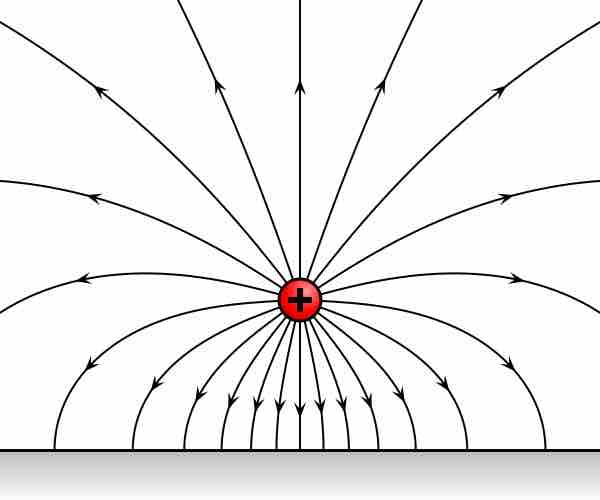
Electric Field Lines of a Positive Charge

Electric field lines emanating from a point where positive electric charge is suspended over a negatively charged infinite sheet. Electric field is a vector field which can be represented as a gradient of a scalar field, called electric potential. Therefore, electric force is a conservative force.

The gradient theorem also has an interesting converse: any conservative vector field can be expressed as the gradient of a scalar field. Just like the gradient theorem itself, this converse has many striking consequences and applications in both pure and applied mathematics

Proof

If $\varphi$ is a differentiable function from some open subset $U$ (of $R^n$) to $R$, and if $r$ is a differentiable function from some closed interval $[a,b]$ to $U$, then by the multivariate chain rule, the composite function $\circ r$ is differentiable on $(a,b)$ and $\frac{d}{dt}(\varphi \circ \mathbf{r})(t)=\nabla \varphi(\mathbf{r}(t)) \cdot \mathbf{r}'(t)$ for for all $t$ in $(a,b)$. Here the $\cdot$ denotes the usual inner product.

Now suppose the domain $U$ of $\varphi$ contains the differentiable curve $\gamma$ with endpoints $p$ and $q$ (oriented in the direction from $p$ to $q$). If $r$ parametrizes for $t$ in $[a,b]$, then the above shows that 

$\begin{aligned} \int_{\gamma} \nabla\varphi(\mathbf{u}) \cdot d\mathbf{u} &=\int_a^b \nabla\varphi(\mathbf{r}(t)) \cdot \mathbf{r}'(t)dt \\ &=\int_a^b \frac{d}{dt}\varphi(\mathbf{r}(t))dt \\ &=\varphi(\mathbf{r}(b))-\varphi(\mathbf{r}(a))\\ &=\varphi\left(\mathbf{q}\right)-\varphi\left(\mathbf{p}\right) \end{aligned}$

where the definition of the line integral is used in the first equality and the fundamental theorem of calculus is used in the third equality.