Examples of homogeneous or nonhomogeneous second-order linear differential equation can be found in many different disciplines, such as physics, economics, and engineering. In this atom, we will learn about the harmonic oscillator, which is one of the simplest yet most important mechanical system in physics.
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force,
Simple harmonic oscillation
If
Therefore, we end up with a homogeneous second-order linear differential equation:
Note that the function
Damped harmonic oscillator
In real oscillators, friction (or damping) slows the motion of the system. In many vibrating systems the frictional force
where
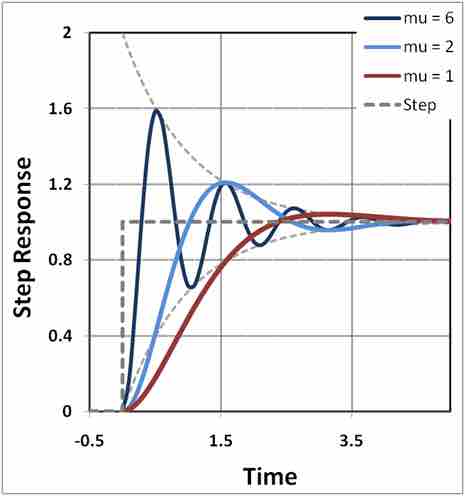
Damped Harmonic Oscillators
A solution of damped harmonic oscillator. Curves in different colors show various responses depending on the damping ratio.
Driven harmonic oscillator: Driven harmonic oscillators are damped oscillators further affected by an externally applied force
It is usually rewritten into the form:
which is a nonhomogeneous second-order linear differential equation.