Series Solutions

The power series method is used to seek a power series solution to certain differential equations. In general, such a solution assumes a power series with unknown coefficients, then substitutes that solution into the differential equation to find a recurrence relation for the coefficients.

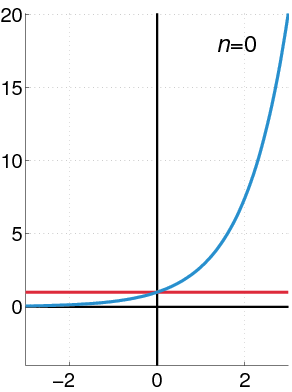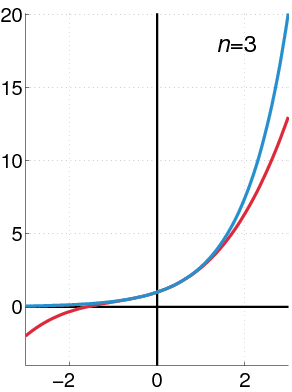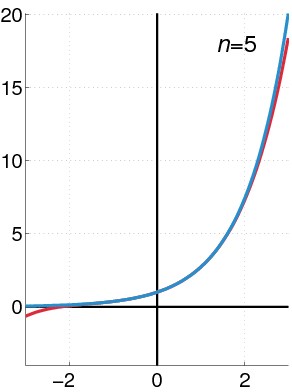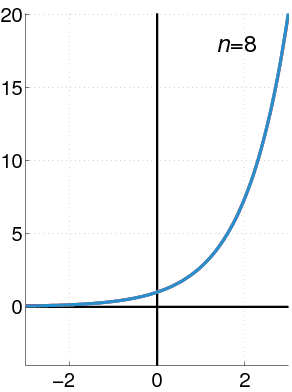
Maclaurin Power Series of an Exponential Function

The exponential function (in blue), and the sum of the first $n+1$ terms of its Maclaurin power series (in red). Using power series, a linear differential equation of a general form may be solved.

Method

Consider the second-order linear differential equation: 

$a_2(z)f''(z)+a_1(z)f'(z)+a_0(z)f(z)=0$

Suppose $a_2$ is nonzero for all $z$. Then we can divide throughout to obtain:

 $\displaystyle{f''+{a_1(z)\over a_2(z)}f'+{a_0(z)\over a_2(z)}f=0}$

Suppose further that $\frac{a_1}{a_2}$ and $\frac{a_1}{a_2}$ are analytic functions. The power series method calls for the construction of a power series solution:

$\displaystyle{f= \sum_{k=0}^\infty A_kz^k}$

After substituting the power series form, recurrence relations for $A_k$ is obtained, which can be used to reconstruct $f$.

Example

Let us look at the case know as Hermit differential equation: 

$f''-2zf'+\lambda f=0\quad (\lambda=1)$

We can try to construct a series solution:

$\displaystyle{f= \sum_{k=0}^\infty A_kz^k \ f'= \sum_{k=0}^\infty kA_kz^{k-1} \ f''= \sum_{k=0}^\infty k(k-1)A_kz^{k-2}}$

substituting these in the differential equation: 

$\begin{aligned} & {} \sum_{k=0}^\infty k(k-1)A_kz^{k-2}-2z \sum_{k=0}^\infty kA_kz^{k-1}+ \sum_{k=0}^\infty A_kz^k=0 \\ & = \sum_{k=0}^\infty k(k-1)A_kz^{k-2}- \sum_{k=0}^\infty 2kA_kz^k+ \sum_{k=0}^\infty A_kz^k \end{aligned}$

making a shift on the first sum:

$\begin{aligned} & = \sum_{k+2=0}^\infty (k+2)((k+2)-1)A_{k+2}z^{(k+2)-2}- \sum_{k=0}^\infty 2kA_kz^k+ \sum_{k=0}^\infty A_kz^k \\ & = \sum_{k=0}^\infty (k+2)(k+1)A_{k+2}z^k- \sum_{k=0}^\infty 2kA_kz^k+ \sum_{k=0}^\infty A_kz^k \\ & = \sum_{k=0}^\infty \left((k+2)(k+1)A_{k+2}+(-2k+1)A_k \right)z^k \end{aligned}$

If this series is a solution, then all these coefficients must be zero, so: 

$(k+2)(k+1)A_{k+2}+(-2k+1)A_k=0$

We can rearrange this to get a recurrence relation for $A_{k+2}$:

$\displaystyle{A_{k+2}={\frac{(2k-1)}{(k+2)(k+1)}A_k}}$

Now, we have:

 $\displaystyle{A_2 = {\frac{-1}{(2)(1)}}A_0={\frac{-1}{2}}A_0, A_3 = {\frac{1}{(3)(2)}} A_1={\frac{1}{6}}A_1}$

and all coefficients with larger indices can be similarly obtained using the recurrence relation. The series solution is:

 $\displaystyle{f=A_0 \left(1+\frac{-1}{2}x^2+\frac{-1}{8}x^4+\frac{-7}{240}x^6+ \cdots \right)\\ \,\quad + A_1 \left(x+\frac{1}{6}x^3+\frac{1}{24}x^5+\frac{1}{112}x^7+ \cdots \right)}$