Applications of Multiple Integrals

As is the case with one variable, one can use the multiple integral to find the average of a function over a given set. Given a set $D \subseteq R^n$ and an integrable function $f$ over $D$, the average value of $f$ over its domain is given by:

 $\displaystyle{\bar{f} = \frac{1}{m(D)} \int_D f(x)\, dx}$

where $m(D)$ is the measure of $D$. Additionally, multiple integrals are used in many applications in physics and engineering. The examples below also show some variations in the notation.

Example 1

In mechanics, the moment of inertia is calculated as the volume integral (triple integral) of the density weighed with the square of the distance from the axis: 

$\displaystyle{I_z = \iiint_V \rho r^2\, dV}$

Example 2

The gravitational potential associated with a mass distribution given by a mass measure $dm$ on three-dimensional Euclidean space $R^3$ is:

 $\displaystyle{V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{\left|\mathbf{x} - \mathbf{r}\right|}\,dm(\mathbf{r})}$

If there is a continuous function $\rho(x)$ representing the density of the distribution at $x$, so that $dm(x) = \rho (x)d^3x$, where $d^3x$ is the Euclidean volume element, then the gravitational potential is:

$\displaystyle{V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{\left|\mathbf{x}-\mathbf{r}\right|}\,\rho(\mathbf{r})\,d^3\mathbf{r}}$

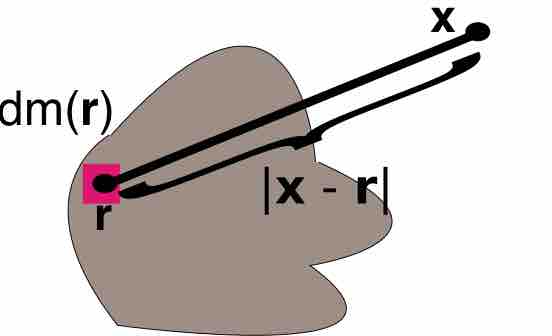
A Mass to be Integrated

Points $\mathbf{x}$ and $\mathbf{r}$, with $\mathbf{r}$ contained in the distributed mass (gray) and differential mass $dm(\mathbf{r})$  located at the point $\mathbf{r}$.

Example 3

In electromagnetism, Maxwell's equations can be written using multiple integrals to calculate the total magnetic and electric fields. In the following example, the electric field produced by a distribution of charges given by the volume charge density $\rho (\vec r)$ is obtained by a triple integral of a vector function: 

$\displaystyle{\vec E = \frac {1}{4 \pi \epsilon_0} \iiint \frac {\vec r - \vec r'}{\| \vec r - \vec r' \|^3} \rho (\vec r')\, {d}^3 r'}$

This can also be written as an integral with respect to a signed measure representing the charge distribution.