The Divergence Theorem

The divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, relates the flow (that is, flux) of a vector field through a surface to the behavior of the vector field inside the surface.

More precisely, the divergence theorem states that the outward flux of a vector field through a closed surface is equal to the volume integral of the divergence over the region inside the surface. Intuitively, it states that the sum of all sources minus the sum of all sinks gives the net flow out of a region. The divergence theorem is an important result for the mathematics of engineering, in particular for electrostatics and fluid dynamics.

In physics and engineering, the divergence theorem is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of calculus. The theorem is a special case of the generalized Stokes' theorem.

Theorem

Suppose $V$ is a subset of $R^n$ (in the case of $n=3$, $V$ represents a volume in 3D space) which is compact and has a piecewise smooth boundary $S$ (also indicated with $\partial V=S$). If $F$ is a continuously differentiable vector field defined on a neighborhood of $V$, then we have:

$\displaystyle{\int \int \int_V \left(\mathbf{\nabla}\cdot\mathbf{F}\right)dV= \oint_S(\mathbf{F}\cdot\mathbf{n})\,dS}$. 

The left side is a volume integral over the volume $V$; the right side is the surface integral over the boundary of the volume $V$.

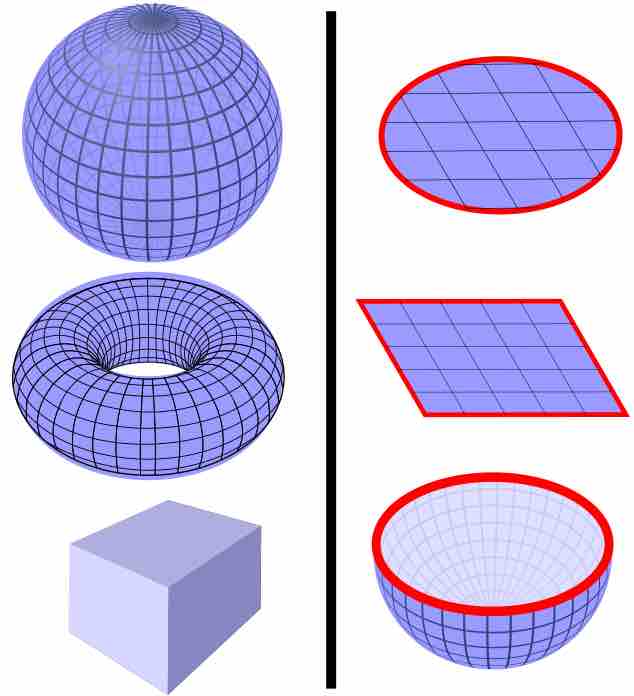
The Divergence Theorem

The divergence theorem can be used to calculate a flux through a closed surface that fully encloses a volume, like any of the surfaces on the left. It can not directly be used to calculate the flux through surfaces with boundaries, like those on the right. (Surfaces are blue, boundaries are red.)

Example

The first equation of the Maxwell's equations is often written as $\nabla \cdot \mathbf{E} = \frac {\rho} {\varepsilon_0}$ in a differential form, where $\rho$ is the electric density. Let's consider a system with a point charge $Q$ located at the origin. We will apply the divergence theorem for a sphere of radius $R$, whose center is also at the origin. Substituting $E$ for $F$ in the relationship of the divergence theorem, the left hand side (LHS) becomes:

 $\displaystyle{\int \int \int_V\left(\mathbf{\nabla}\cdot\mathbf{E}\right)dV = \int \int \int_V \left(\frac{\rho}{\varepsilon_0}\right)dV = \frac{Q}{\varepsilon_0}}$

The surface integral on the right hand side (RHS) becomes: 

$\displaystyle{\int_S(\mathbf{E}\cdot\mathbf{n})\,dS = 4\pi R^2 E}$

Combining RHS and LHS, we get:

 $\displaystyle{E = \frac{Q}{4\pi \varepsilon_0 R^2}}$

This is simply the electric field for the Coulomb force.