Stokes' Theorem

The generalized Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Stokes' theorem says that the integral of a differential form $\omega$ over the boundary of some orientable manifold $\Omega$ is equal to the integral of its exterior derivative $d\omega$ over the whole of $\Omega$, i.e.:

$\displaystyle{\int_{\partial \Omega}\omega=\int_{\Omega}\mathrm {d}\omega}$

The Kelvin–Stokes theorem, also known as the curl theorem, is a theorem in vector calculus on $R^3$. Given a vector field, the theorem relates the integral of the curl of the vector field over some surface to the line integral of the vector field around the boundary of the surface. The Kelvin–Stokes theorem is a special case of the "generalized Stokes' theorem." If $\mathbf{F}$ is a smooth vector field on $R^3$, then:

$\displaystyle{\oint_{\Gamma} \mathbf{F}\, d\Gamma = \iint_{S} \nabla\times\mathbf{F}\, dS}$

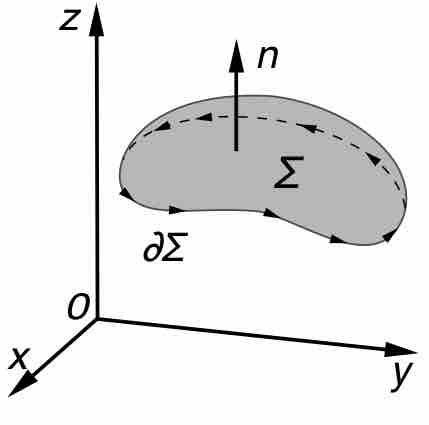
Kelvin-Stokes' Theorem

An illustration of the Kelvin–Stokes theorem, with surface $\Sigma$, its boundary $\partial$, and the "normal" vector $\mathbf{n}$.

Application in Electromagnetism

Electric field is a conservative vector field. Therefore, electric field can be written as a gradient of a scalar field: 

$\mathbf{E} = - \nabla {\varphi}$

Applying the Kelvin-Stokes theorem and substituting in $\oint_{\Gamma} \mathbf{F}\, d\Gamma = \iint_{S} \nabla\times\mathbf{F}\, dS$, we get:

$\displaystyle{\oint_{\Gamma} \mathbf{E}\, d\Gamma = -\iint_{S} \nabla\times (\nabla \varphi) \, dS}$

Since $\nabla \times \nabla f = 0$ for an arbitrary function $f$, we derive:

$\displaystyle{\oint_{\Gamma} \mathbf{E}\, d\Gamma = 0}$

As we have seen in our previous atom on gradient theorem, this simply means:

$\displaystyle{\int_P \mathbf{E}\cdot d\mathbf{r}=\varphi(B)-\varphi(A)}$

which is equivalent to saying that work done by the electric field only depends on the initial and final point of the motion. The scalar field $\varphi$ in the case of electromagnetism is called electric potential.