Surface Integrals of Vector Fields

Consider a vector field $\mathbf{v}$ on $S$; that is, for each $\mathbf{x}$ in $S$, $\mathbf{v}(\mathbf{x})$ is a vector. The surface integral of vector fields can be defined component-wise according to the definition of the surface integral of a scalar field; the result is a vector. This applies, for example, in the expression of the electric field at some fixed point due to an electrically charged surface, or the gravity at some fixed point due to a sheet of material.

Alternatively, if we integrate the normal component of the vector field, the result is a scalar. Imagine that we have a fluid flowing through $S$, such that $\mathbf{v}(\mathbf{x})$ determines the velocity of the fluid at $\mathbf{x}$. The flux is defined as the quantity of fluid flowing through $S$ in unit amount of time.

This illustration implies that if the vector field is tangent to $S$ at each point, then the flux is zero, because the fluid just flows in parallel to $S$, and neither in nor out. This also implies that if $\mathbf{v}$ does not just flow along $S$—that is, if $\mathbf{v}$ has both a tangential and a normal component—then only the normal component contributes to the flux. Based on this reasoning, to find the flux, we need to take the dot product of $\mathbf{v}$ with the unit surface normal to $S$, at each point, which will give us a scalar field, and integrate the obtained field as above. We find the formula:

$\displaystyle{\int_S {\mathbf v}\cdot \,d{\mathbf {S}} = \int_S {\mathbf v}\cdot {\mathbf n}\,dS=\iint_T {\mathbf v}(\mathbf{x}(s, t))\cdot \left({\partial \mathbf{x} \over \partial s}\times {\partial \mathbf{x} \over \partial t}\right) ds\, dt}$

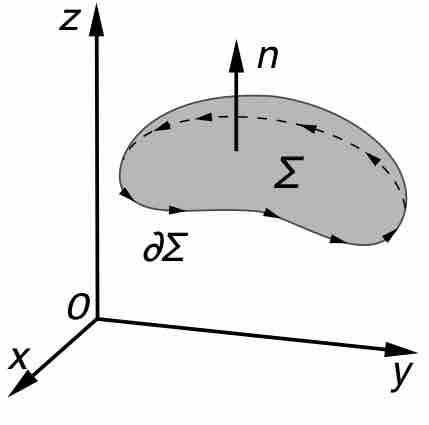
Kelvin-Stokes' Theorem

An illustration of the Kelvin–Stokes theorem, with surface $\Sigma$, its boundary $\partial$, and the "normal" vector $n$.

The cross product on the right-hand side of this expression is a surface normal determined by the parametrization. This formula defines the integral on the left (note the dot and the vector notation for the surface element).

Example

An electric field from a point charge ($Q$) is given as:

 $\displaystyle{\mathbf{E} = \frac{Q}{4\pi\varepsilon_0} \frac{\mathbf{\hat{r}}}{|\mathbf{r}|^2}}$

where $r$ is the position vector and $\hat{r}$ is a unit vector in radial direction. If the charge is located at the center of a sphere with a radius $R$, the surface integral of the electric field over the surface is calculated at the following: 

$\displaystyle{\int_S {\mathbf{E}} \cdot d\mathbf{S} = \frac{Q}{4\pi\varepsilon_0} \int_S \frac{1}{\left|\mathbf{r}\right|^2} dS = \frac{Q}{\varepsilon_0}}$