Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus in more than one variable : the differentiated and integrated functions involve multiple variables, rather than just one. Multivariable calculus can be applied to analyze deterministic systems that have multiple degrees of freedom. Functions with independent variables corresponding to each of the degrees of freedom are often used to model these systems, and multivariable calculus provides tools for characterizing the system dynamics.
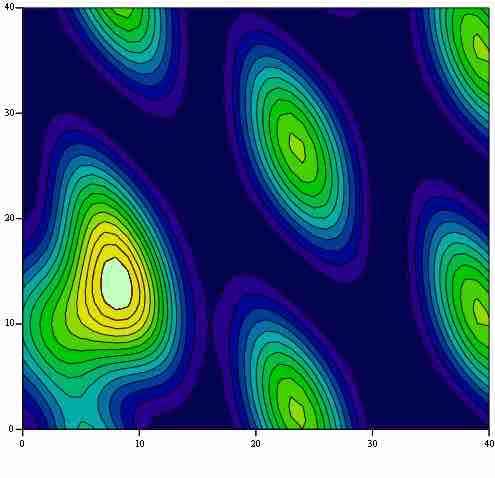
A Scalar Field
A scalar field shown as a function of
Multivariable calculus is used in many fields of natural and social science and engineering to model and study high-dimensional systems that exhibit deterministic behavior. Non-deterministic, or stochastic, systems can be studied using a different kind of mathematics, such as stochastic calculus. Quantitative analysts in finance also often use multivariate calculus to predict future trends in the stock market.
As we will see, multivariable functions may yield counter-intuitive results when applied to limits and continuity. Unlike a single variable function
We have also studied theorems linking derivatives and integrals of single variable functions. The theorems we learned are gradient theorem, Stokes' theorem, divergence theorem, and Green's theorem. In a more advanced study of multivariable calculus, it is seen that these four theorems are specific incarnations of a more general theorem, the generalized Stokes' theorem, which applies to the integration of differential forms over manifolds.