What is a Vector Valued Function?
Also called vector functions, vector valued functions allow you to express the position of a point in multiple dimensions within a single function. These can be expressed in an infinite number of dimensions, but are most often expressed in two or three. The input into a vector valued function can be a vector or a scalar. In this atom we are going to introduce the properties and uses of the vector valued functions.
Properties of Vector Valued Functions
A vector valued function allows you to represent the position of a particle in one or more dimensions. A three-dimensional vector valued function requires three functions, one for each dimension. In Cartesian form with standard unit vectors (i,j,k), a vector valued function can be represented in either of the following ways:
where
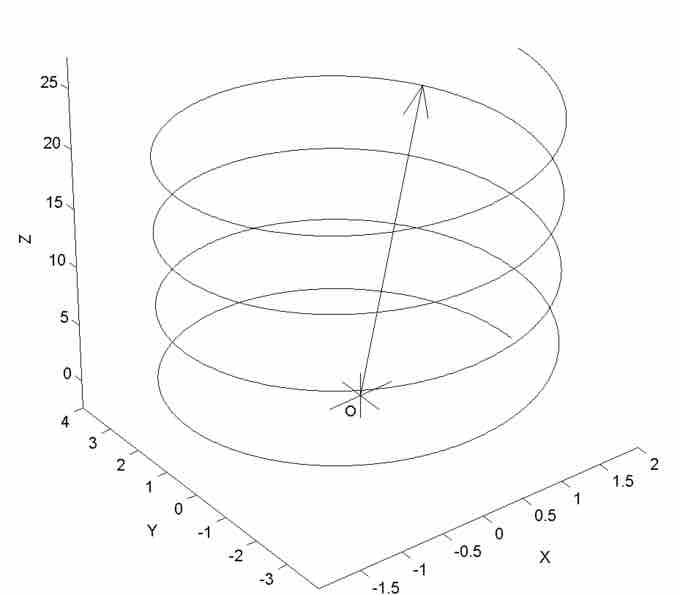
Vector-Valued Function
This a graph of a parametric curve (a simple vector-valued function with a single parameter of dimension
This can be broken down into three separate functions called component functions:
If you were to take a cross section, with the cut perpendicular to any of the three axes, you would see the graph of that function. For example, if you were to slice the three-dimensional shape perpendicular to the
Example
For this example, we will use time as our parameter. The following vector valued function represents time,
This function is representing a position. Therefore, if we take the derivative of this function, we will get the velocity:
If we differentiate a second time, we will be left with acceleration: