The maximum and minimum of a function, known collectively as extrema, are the largest and smallest values that the function takes at a point either within a given neighborhood (local or relative extremum) or on the function domain in its entirety (global or absolute extremum).
Finding Maxima and Minima of Multivariable Functions
The second partial derivative test is a method in multivariable calculus used to determine whether a critical point
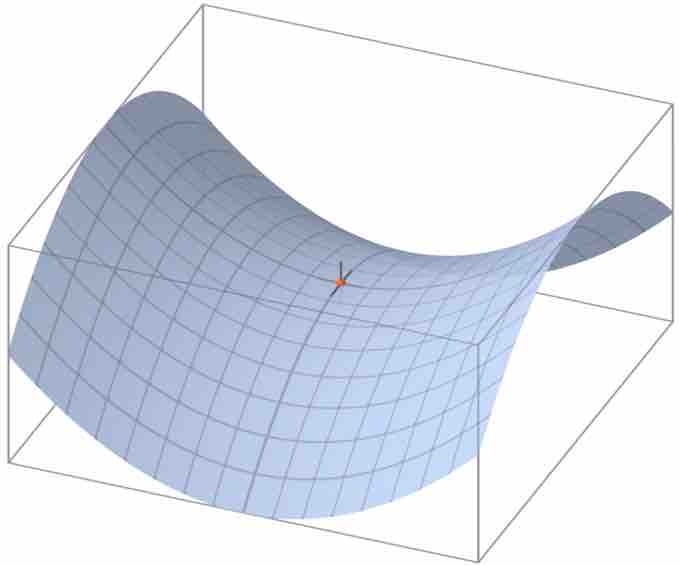
Saddle Point
A saddle point on the graph of
For a function of two variables, suppose that
- If
$M(a,b)>0$ and$f_{xx}(a,b)>0$ , then$(a,b)$ is a local minimum of$f$ . - If M(a,b)>0M(a,b)>0 and fxx(a,b)<0f_{xx}(a,b)<0, then
$(a,b)$ is a local maximum of$f$ . - If
$M(a,b)<0$ , then$(a,b)$ is a saddle point of$f$ . - If
$M(a,b)=0$ , then the second derivative test is inconclusive.
There are substantial differences between functions of one variable and functions of more than one variable in the identification of global extrema. For example, if a bounded differentiable function