The directional derivative of a multivariate differentiable function along a given vector
Definition
The directional derivative of a scalar function
If the function
We can imagine the directional derivative
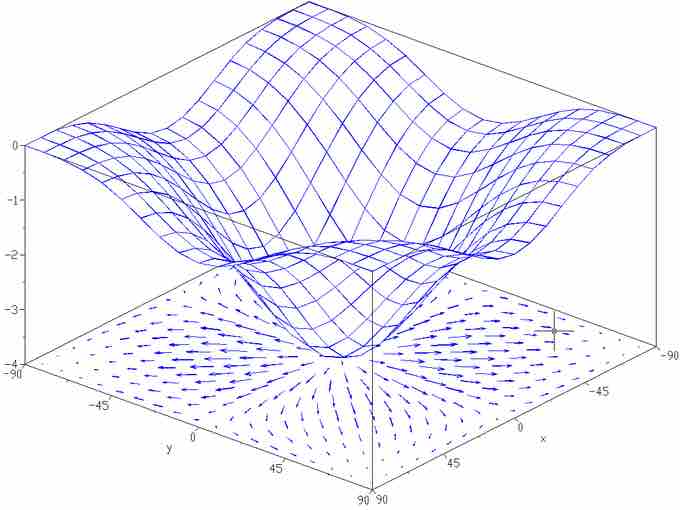
Gradient of a Function
The gradient of the function
Properties
Many of the familiar properties of the ordinary derivative hold for the directional derivative.
The Sum Rule
The Constant Factor Rule
For any constant
The Product Rule (or Leibniz Rule)
The Chain Rule
If