Cylinder
A cylinder (from Greek "roller" or "tumbler") is one of the most basic curvilinear geometric shapes. The surface is formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder. The surface area and the volume of a cylinder have been known since antiquity. A cylinder can be seen as a polyhedral limiting case of an
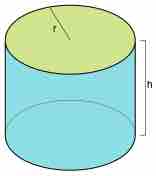
Cylinder
A right circular cylinder with radius
In common use, a cylinder is taken to mean a finite section of a right circular cylinder, i.e. the cylinder with the generating lines perpendicular to the bases, with its ends closed to form two circular surfaces. If the cylinder has a radius
Quadric Surface
A quadric, or quadric surface, is any
Cylinders, spheres, ellipsoids, etc. are special cases of quadric surfaces.
Examples
Ellipsoid:
Sphere:
Elliptic paraboloid:
Cone:
Parabolic cylinder:
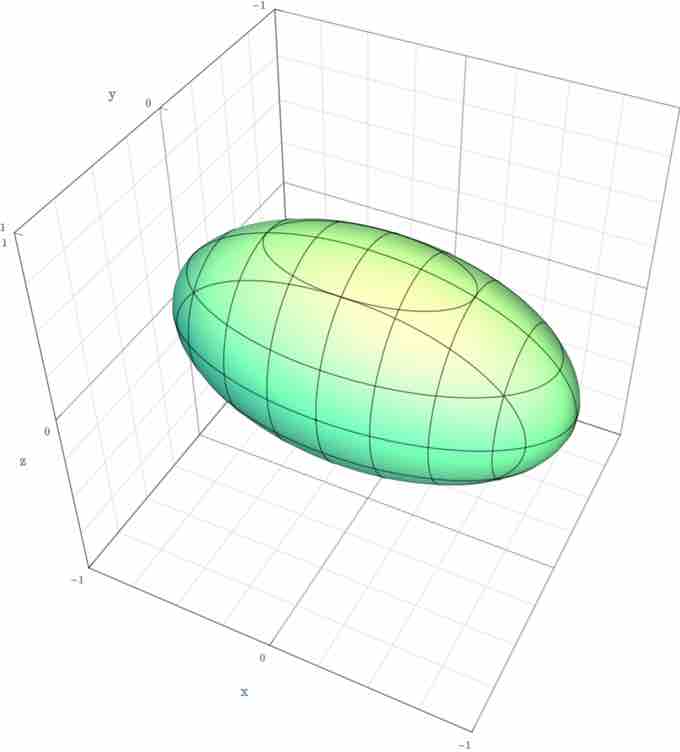
Ellipsoid
An ellipsoid given as