Cylindrical and Spherical Coordinates

While Cartesian coordinates have many applications, cylindrical and spherical coordinates are useful when describing objects or phenomena with specific symmetries.

Cylindrical Coordinates

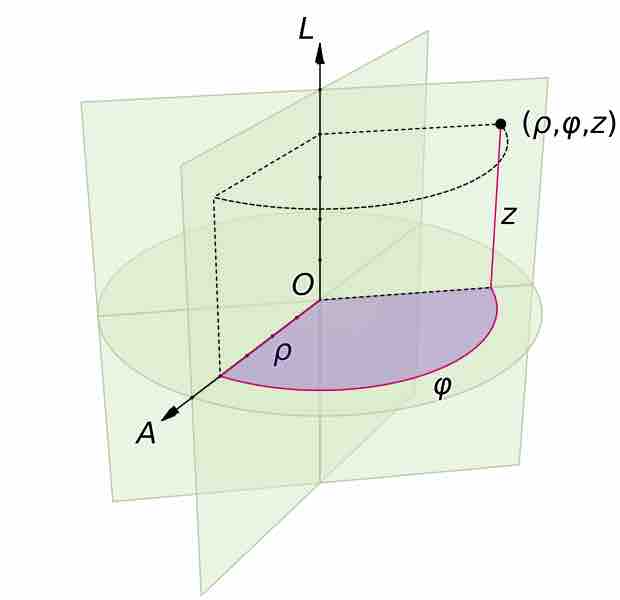
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis. The latter distance is given as a positive or negative number, depending on which side of the reference plane faces the point.

Cylindrical Coordinate System

A cylindrical coordinate system with origin $O$, polar axis $A$, and longitudinal axis $L$. The dot is the point with radial distance $\rho = 4$, angular coordinate $\varphi = 130$ degrees, and height $z = 4$.

Cylindrical coordinates are useful in connection with objects and phenomena that have some rotational symmetry about the longitudinal axis, such as water flow in a straight pipe with a round cross-section, heat distribution in a metal cylinder, electromagnetic fields produced by an electric current in a long, straight wire, and so on.

For the conversion between cylindrical and Cartesian coordinate co-ordinates, it is convenient to assume that the reference plane of the former is the Cartesian $xy$-plane (with equation $z = 0$), and the cylindrical axis is the Cartesian $z$-axis. Then the $z$ coordinate is the same in both systems, and the correspondence between cylindrical $(\rho,\varphi)$ and Cartesian $(x,y)$ are the same as for polar coordinates, namely $x = \rho \cos \varphi; \, y = \rho \sin \varphi$. In the reverse transformation:

$\rho = \sqrt{x^{2}+y^{2}}$

$\varphi = \begin{cases} 0 & \mbox{if } x = 0 \mbox{ and } y = 0\\ \arcsin(\frac{y}{\rho}) & \mbox{if } x \geq 0 \\ -\arcsin(\frac{y}{\rho}) + \pi & \mbox{if } x < 0\\ \end{cases}$

Spherical Coordinates

A spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. Spherical coordinates are useful in connection with objects and phenomena that have spherical symmetry, such as an electric charge located at the origin.

Spherical Coordinate System

Spherical coordinates ($r$, $\theta$, $\varphi$) as often used in mathematics: radial distance $r$, azimuthal angle $\theta$, and polar angle $\varphi$. The meanings of $\theta$ and $\varphi$ have been swapped compared to the physics convention.

The spherical coordinates (radius $r$, inclination $\theta$, azimuth $\varphi$) of a point can be obtained from its Cartesian coordinates ($x$, $y$, $z$) by the formulae:

$r=\sqrt{x^2+y^2+z^2} \\ \theta = \mbox{arccos}\left(\frac{z}{r}\right) \\ \varphi = \mbox{arctan}\left(\frac{y}{x}\right)$

In reverse:

$x=r \, \sin\theta \, \cos\varphi \\ y=r \, \sin\theta \, \sin\varphi \\ z=r \, \cos\theta$