We studied how double integrals can be evaluated over a rectangular region. But there is no reason to limit the domain to a rectangular area. The integral domain can be of any general shape. In this atom, we will study how to formulate such an integral.
This method is applicable to any domain
- the projection of
$D$ onto either the$x$ -axis or the$y$ -axis is bounded by the two values,$a$ and$b$ . - any line perpendicular to this axis that passes between these two values intersects the domain in an interval whose endpoints are given by the graphs of two functions,
$\alpha$ and$\beta$ .
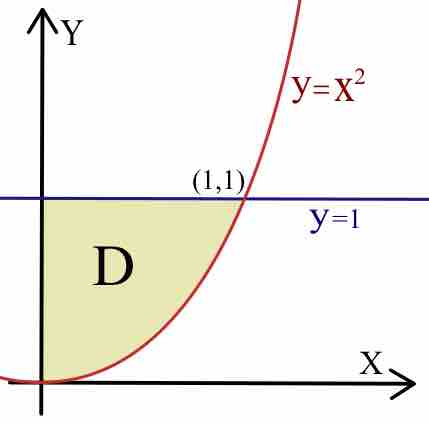
Example
Consider the following region:
Calculate
Double Integral
Double integral over the normal region
It is now possible to apply the formula:
(At first the second integral is calculated considering