The tangent line (or simply the tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Similarly, the tangent plane to a surface at a given point is the plane that "just touches" the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized.
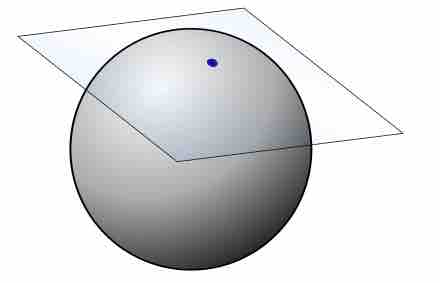
Tangent Plane to a Sphere
The tangent plane to a surface at a given point is the plane that "just touches" the surface at that point.
Equations
When the curve is given by
where
The tangent plane to a surface at a given point
where
Linear Approximation
Since a tangent plane is the best approximation of the surface near the point where the two meet, tangent plane can be used to approximate the surface near the point. The approximation works well as long as the point