Planetary Motion According to Kepler and Newton

Johannes Kepler describes planetary motion with three laws: 1. The orbit of every planet is in an elliptical shape, with the Sun being at one of the two foci of this ellipse, called the occupied focus; 2. If a line where to be drawn from the planet to the Sun, that line would sweep out an equal amount of area during equal intervals of time; 3. The square of the orbital period is proportional to the cube of the semi-major axis of the planet's orbit.

Kepler's First Law

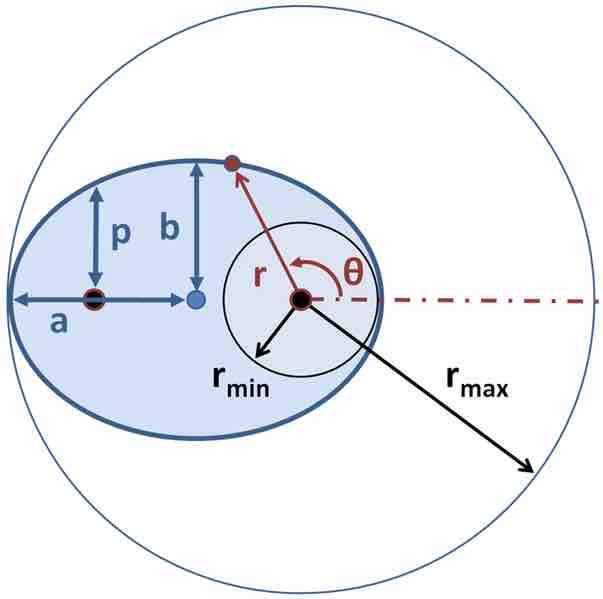
As we already stated, the first law of planetary motion states that the orbit of every planet is an ellipse with the Sun at one focus. In order to discuss this law, and the laws that follow, we should examine the components of an ellipse a bit more closely.

The eccentricity of an ellipse tells you how stretched out the ellipse is. The eccentricity can be from 0 to 1. If the eccentricity is equal to zero, that means it is a circle. In Kepler's time, the extremes of planetary eccentricity were Venus, 0.007, and Mercury, 0.2. The eccentricity is what makes an ellipse different from a circle.

$\displaystyle{r=\frac{p}{1+{\Sigma} \cdot \cos{\theta}}}$

where $p$ is the semi-latus rectum, $\Sigma$ is the eccentricity, $r$ is the distance between the planet and the sun, and $\theta$ is the angle between the position of the planet and its most direct route to the Sun. The minimum distance occurs when the angle is 0. The maximum distance occurs when the angle is 180 degrees. These values are important because the equation for eccentricity is:

$\displaystyle{\Sigma=\frac{r_{\text{max}}-r_{\text{min}}}{r_{\text{max}}+r_{\text{min}}}}$

The semi-major axis, $a$, can be found as follows: 

$\displaystyle{a=\frac{p}{1-\Sigma^2}}$

The semi-minor axis, $b$, can be found as follows:

 $\displaystyle{b=\frac{p}{\sqrt{1-\Sigma^2}}}$

The area of an ellipse is found as follows: 

$A=\pi \cdot a \cdot b$

Ellipse

The important components of an ellipse are as follows: semi-major axis $a$, semi-minor axis $b$, semi-latus rectum $p$, the center of the ellipse, and its two foci marked by large dots. For $\theta = 0$ degrees, $r = r_{\text{min}}$ and for $\theta = 180$ degrees, $r = r_{\text{max}}$.

Kepler's Second Law

The second law of planetary motion states that in an amount of time, $t$, a line from the planet to the Sun will sweep out a triangle having a base of $r$ and a height of $r \cdot d\theta$. Therefore, the area of this triangle is:

$\displaystyle{dA=\frac{1}{2} \cdot r \cdot rd\theta}$

and the ratio of the area of this triangle to the time elapsed is: 

$\displaystyle{\frac{dA}{dt}=\frac{1}{2} \cdot r^2 \cdot \frac{d\theta}{dt}}$

As the planet moves closer to the Sun, it speeds up. This allows the triangle to have an equal area in an equal amount of time regardless of position of the planet. As we learned in the first section, the area of an ellipse is $\pi \cdot a \cdot b$. Therefore, the period ($P$) of the ellipse satisfies: 

$\pi \cdot a \cdot b=P \cdot \frac{1}{2} \cdot r^2 \cdot \theta\\ r^2\theta=n\cdot a\cdot b$

where $\theta$ is the angular velocity with respect to time, and $n$ is the mean motion of the planet around the Sun.

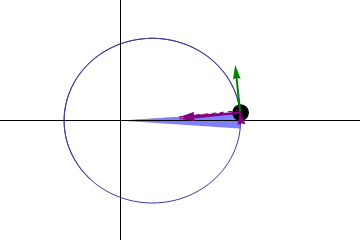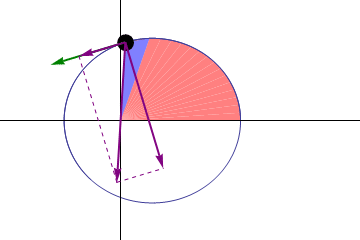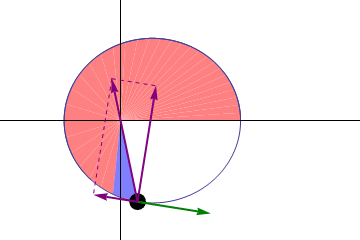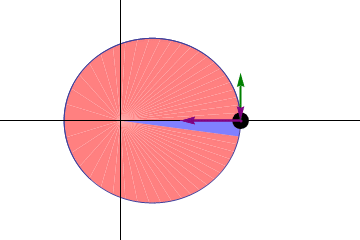
The Second Law

Illustration of Kepler's second law. The planet moves faster near the Sun so that the same area is swept out in a given time as it would be at larger distances, where the planet moves more slowly. The green arrow represents the planet's velocity, and the purple arrows represent the force on the planet.

Kepler's Third Law

Kepler's third law describes the relationship between the distance of the planets from the Sun, and their orbits period. $P^2 \propto a^3$ , with a constant of proportionality of:

$\displaystyle{\frac{P^2_{\text{planet}}}{a^3_{\text{planet}}} = \frac{P^2_{\text{earth}}}{a^3_{\text{earth}}} = 1 \frac{\text{year}}{\text{AU}}}$

where AU is an astronomical unit. In the case of a circular orbit, the proportionality constant is as follows:

$\displaystyle{\frac{4\pi^2}{T^2}=\frac{GM}{R^3}}$

where $T$ is the period, $G$ is the gravitational constant, and $R$ is the distance between the center of mass of the two bodies.

How does Newton Relate to Kepler?

Newton derived his theory of the acceleration of a planet from Kepler's first and second laws. Newton theorized that the direction of a planet is always towards the Sun. In addition, the magnitude of the acceleration is inversely proportional to the square of its distance from the Sun. From this, Newton defined the force acting on a planet as the product of its mass and acceleration. Therefore, by Newton's law, every planet is attracted to the Sun, and the force acting on a planet is directly proportional to the mass and inversely proportional to the square of its distance from the Sun.