We have learned how to find the minimum and maximum in multivariable functions. As previously mentioned, finding extrema can be a challenge with regard to multivariable functions. In particular, we learned about the second derivative test, which is a criterion for determining whether a given critical point of a real function of one variable is a local maximum or a local minimum, using the value of the second derivative at the point. In this atom, we will find extrema for a function with two variables.
Example
Find and label the critical points of the following function:
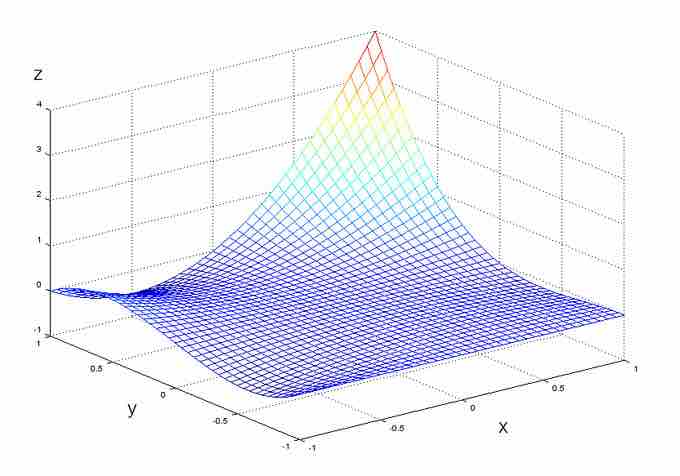
Plot of $z = (x+y)(xy+xy^2)$
The maxima and minima of this plot cannot be found without extensive calculation.
To solve this problem we must first find the first partial derivatives of the function with respect to
Looking at
We plug the first solution,
There were other possibilities for
So
So
Let's list all the critical values now:
Now we have to label the critical values using the second derivative test. Plugging in all the different critical values we found to label them, we have:
-
$D(0, 0) = 0$ -
$D(0, -1) = -1$ -
$D(1, -1) = -1$ -
$D\left(\frac{3}{8}, -\frac{3}{4}\right) = 0.210938$
We can now label some of the points:
- at (0, −1),
$f(x, y)$ has a saddle point - at (1, −1),
$f(x, y)$ has a saddle point - at
$\left(\frac{3}{8}, -\frac{3}{4}\right)$ $f(x, y)$ has a local maximum, since$f_{xx} = -\frac{3}{8} < 0$
At the remaining point we need higher-order tests to find out what exactly the function is doing.