Special Right Triangles: How to Recognize and Calculate Them

Learn the rules for special right triangles and how to solve the different types

Last Updated: February 17, 2023 References

What is a special right triangle?

|

Angle-Based Special Right Triangles

|

Side-Based Special Right Triangles

Special right triangles are an oddity in math. Whereas most triangles have sides and angles that are hard to calculate, special right triangles have unique properties that make them easier to work with. They can be a bit confusing if you’ve never encountered them before—especially if math isn’t your strong suit. But special right triangles are actually pretty simple. They follow regular patterns, making them easy to recognize once you learn the basics. Here’s a guide for identifying special right triangles, plus some tips on doing calculations with them.

Things You Should Know

Special right triangles have unique properties that make calculations easier.
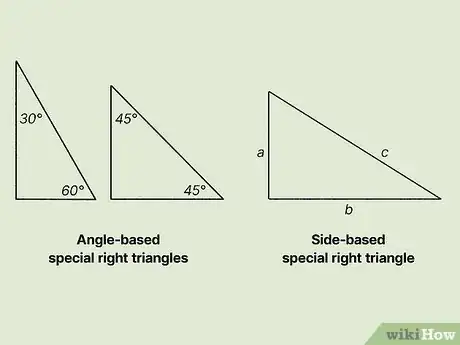
There are two types of special right triangles: angle-based and side-based.
Angle-based special right triangles have three angles that can be represented as integers.
Side-based special right triangles have three sides that can be represented as integers.

Section 1 of 3:

What is a special right triangle?

A special right triangle is a right triangle with angles or sides that make calculations simpler. The lengths of their sides are highly predictable and follow specific patterns, so you don’t need to use equations like the Pythagorean theorem. There are two types of special right triangles: angle-based and side-based.
- Angle-based special right triangles have three angles that can be represented as integers.^{[1]
  X
  Research source} There are only two angle-based special right triangles: the 30-60-90 triangle, and the 45-45-90 triangle.^{[2]
  X
  Research source}
- Side-based special right triangles have three sides that can be represented as integers.^{[3]
  X
  Research source} Each group of three integers is called a Pythagorean triple. There are an infinite number of Pythagorean triples—which means there are also an infinite number of side-based special right triangles.

Section 2 of 3:

Angle-Based Special Right Triangles

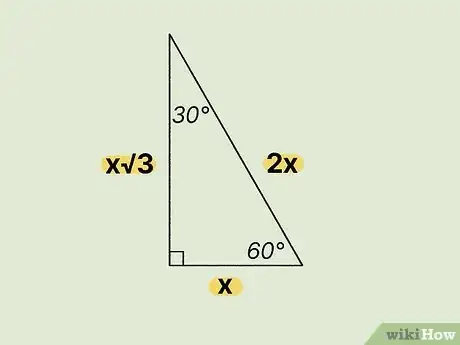
1
30-60-90 Triangle. As the name suggests, this triangle has angles equal to 30, 60, and 90 degrees. What makes it “special” is that its sides can be represented as 1, √3, and 2. More accurately, the sides have a ratio of x, x√3, and 2x with respect to each other, where “x” equals the length of the shortest side.^{[4]
X
Research source}
- Example: If the shortest side is 10 cm long, we can say that x=10 cm. We can calculate the length of two remaining sides by multiplying their coefficients by 10 cm: 10cm*√3 and 2*10cm (√3 = roughly 1.732). This gives us a triangle with sides equal to 10 cm, 17.32 cm, and 20 cm.
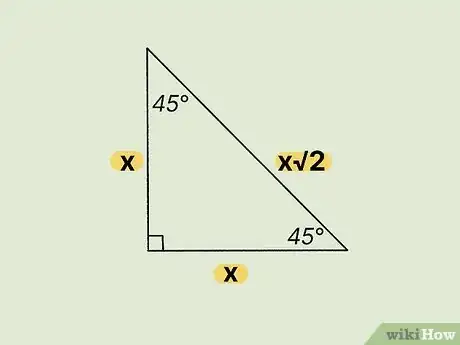
2
45-45-90 Triangle. This one has angles equal to 45, 45, and 90 degrees. Its sides can be represented as 1, 1, and √2, meaning its sides have a ratio of x, x, and x√2 with respect to each other. Note that two sides are labeled “x”. This means that they are the same length.^{[5]
X
Research source}
- Example: If x=50 m, then we know that two side of the triangle are 50 m long. To calculate the length of the remaining side, we multiple the coefficient √2 by 50 m (√2 = roughly 1.414). This gives us a triangle with sides equal to 50 m, 50 m, and 70.7 m.

Section 3 of 3:

Side-Based Special Right Triangles

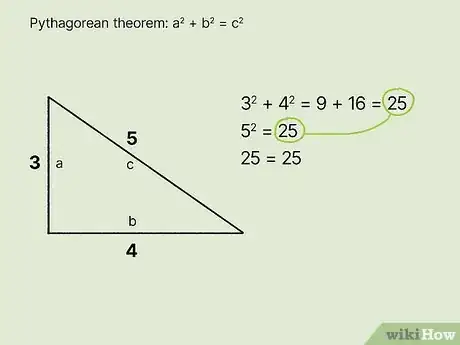
1
Side-based special right triangles have sides that can be represented by integers. The 3-4-5 triangle is one example. Using the Pythagorean theorem, you’ll see that 3² + 4² = 25. Then, √25 = 5, which is an integer. This makes 3-4-5 a “Pythagorean triple.”^{[6]
X
Research source}
- Common Pythagorean triples: 5-12-13, 7-24-25, 8-15-17, 20-21-29, and 28-45-53. There are infinitely many more.
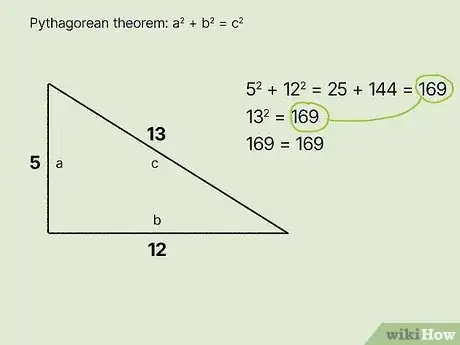
2
5-12-13 Triangle (example). Using the Pythagorean theorem, you’ll see that 5² + 12² = 169. Meanwhile, √169 = 13, which is a perfect integer. Therefore, the 5-12-13 triangle is a side-based special right triangle.^{[7]
X
Research source}
- The numbers 3-4-5 represent the ratio of the sides with respect to each other. These ratios are 3/4, 3/5, 4/3, 4/5, 5/3, and 5/4.
- If, for example, you double the sides to 6-8-10, the ratios remain the same: 6/8 = 3/4, 6/10 = 3/5, and so on. Therefore, a 6-8-10 triangle is equivalent to the 3-4-5 triangle.
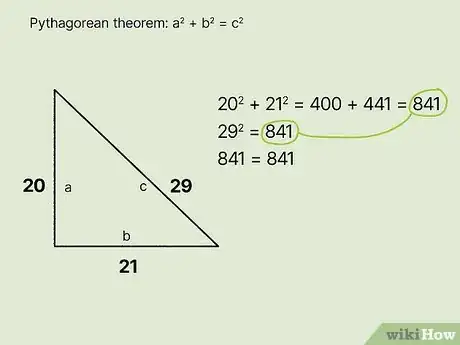
3
20-21-29 Triangle (example). The Pythagorean theorem shows that 20² + 21² = 841. Then, √841 = 29. This makes the 20-21-29 triangle a side-based special right triangle.^{[8]
X
Research source}
- Remember: the numbers 20-21-29 represent the ratios of the sides with respect to each other.