How to Calculate the Radius of a Circle

Last Updated: February 3, 2023 References

The radius of a circle is the distance from the center of the circle to any point on its circumference.^{[1]
X
Research source} The easiest way to find the radius is by dividing the diameter in half. If you don’t know the diameter but you know other measurements, such as the circle’s circumference ( $C=2\pi r$ ) or area ( $A=\pi r^{2}$ ), you can still find the radius by using the formulas and isolating the $r$ variable.

Method 1

Method 1 of 4:

Using the Circumference

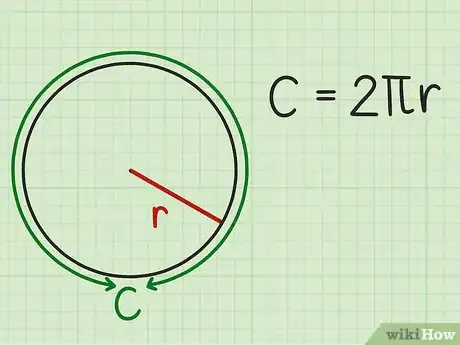
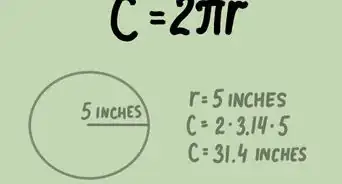
1
Write down the circumference formula. The formula is
$C=2\pi r$
, where $C$ $C$ equals the circle’s circumference, and $r$ $r$ equals its radii^{[2]
X
Research source}
- The symbol $\pi$ ("pi") is a special number, roughly equal to 3.14. You can either use that estimate (3.14) in calculations, or use the $\pi$ symbol on a calculator.
2
Solve for r. Use algebra to change the circumference formula until r (radius) is alone on one side of the equation:

Example
$C=2\pi r$
${\frac {C}{2\pi }}={\frac {2\pi r}{2\pi }}$
${\frac {C}{2\pi }}=r$
$r={\frac {C}{2\pi }}$

Advertisement
3
Plug the circumference into the formula. Whenever a math problem tells you the circumference C of a circle, you can use this equation to find the radius r. Replace C in the equation with the circumference of the circle in your problem:

Example
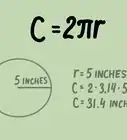
If the circumference is 15 centimeters, your formula will look like this: $r={\frac {15}{2\pi }}$ centimeters
4
Round to a decimal answer. Enter your result in a calculator with the $\pi$ button and round the result. If you don't have a calculator, calculate it by hand, using 3.14 as a close estimate for $\pi$ .

Example
$r={\frac {15}{2\pi }}=$ about ${\frac {7.5}{2*3.14}}=$ approximately 2.39 centimeters

Method 2

Method 2 of 4:

Using the Area

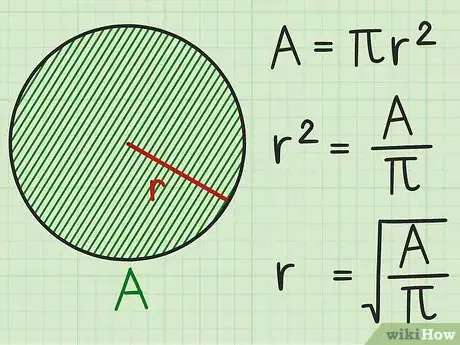
1
Set up the formula for the area of a circle. The formula is
$A=\pi r^{2}$
, where $A$ equals the area of the circle, and $r$ equals the radius.^{[3]
X
Research source}
2
Solve for the radius. Use algebra to get the radius r alone on one side of the equation:

Example
Divide both sides by $\pi$ :
$A=\pi r^{2}$
${\frac {A}{\pi }}=r^{2}$
Take the square root of both sides:
${\sqrt {\frac {A}{\pi }}}=r$
$r={\sqrt {\frac {A}{\pi }}}$
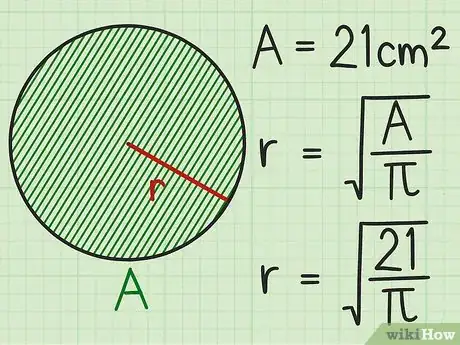
3
Plug the area into the formula. Use this formula to find the radius when the problem tells you the area of the circle. Substitute the area of the circle for the variable $A$ .

Example
If the area of the circle is 21 square centimeters, the formula will look like this: $r={\sqrt {\frac {21}{\pi }}}$
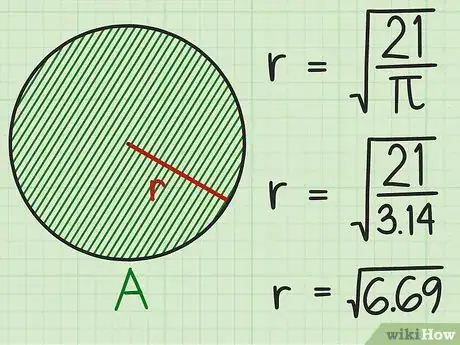
4
Divide the area by $\pi$ . Begin solving the problem by simplifying the portion under the square root ( ${\frac {A}{\pi }})$ . Use a calculator with a $\pi$ key if possible. If you don't have a calculator, use 3.14 as an estimate for $\pi$ .

Example
If using 3.14 for $\pi$ , you would calculate:
$r={\sqrt {\frac {21}{3.14}}}$
$r={\sqrt {6.69}}$
If your calculator allows you to enter the whole formula on one line, that will give you a more accurate answer.
5
Take the square root.
You will likely need a calculator to do this
, because the number will be a decimal. This value will give you the radius of the circle.

Example
$r={\sqrt {6.69}}=2.59$ . So, the radius of a circle with an area of 21 square centimeters is about 2.59 centimeters.
Areas always use square units (like square centimeters), but the radius always uses units of length (like centimeters). If you keep track of units in this problem, you'll notice that ${\sqrt {cm^{2}}}=cm$ .

Method 3

Method 3 of 4:

Using the Diameter

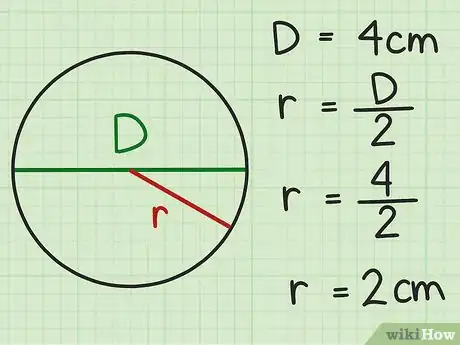
1
Check the problem for a diameter. If the problem tells you the diameter of the circle, it's easy to find the radius. If you are working with an actual circle,
measure the diameter by placing a ruler so its edge passes straight through the circle's center
, touching the circle on both sides.^{[4]
X
Research source}
- If you're not sure where the circle center is, put the ruler down across your best guess. Hold the zero mark of the ruler steady against the circle, and slowly move the other end back and forth around the circle's edge. The highest measurement you can find is the diameter.
- For example, you might have a circle with a diameter of 4 centimeters.
2
Divide the diameter by two. A circle's
radius is always half the length of its diameter.
^{[5]
X
Research source}
- For example, if the diameter is 4 cm, the radius equals 4 cm ÷ 2 = 2 cm.
- In math formulas, the radius is r and the diameter is d. You might see this step in your textbook as $r={\frac {d}{2}}$ .

Method 4

Method 4 of 4:

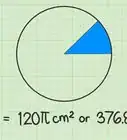
Using the Area and Central Angle of a Sector

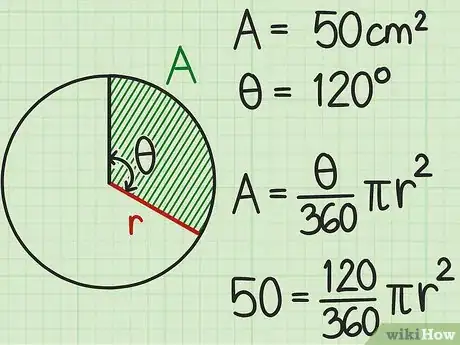
1
Set up the formula for the area of a sector. The formula is
$A_{sector}={\frac {\theta }{360}}(\pi )(r^{2})$
, where $A_{sector}$ equals the area of the sector, $\theta$ equals the central angle of the sector in degrees, and $r$ equals the radius of the circle.^{[6]
X
Research source}
2
Plug the sector’s area and central angle into the formula. This information should be given to you.
Make sure you have the area of the sector, not the area for the circle.
Substitute the area for the variable $A_{sector}$ and the angle for the variable $\theta$ .

Example
If the area of the sector is 50 square centimeters, and the central angle is 120 degrees, you would set up the formula like this:
$50={\frac {120}{360}}(\pi )(r^{2})$ .
3
Divide the central angle by 360. This will tell you what fraction of the entire circle the sector represents.

Example
${\frac {120}{360}}={\frac {1}{3}}$ . This means that the sector is ${\frac {1}{3}}$ of the circle.
Your equation should now look like this: $50={\frac {1}{3}}(\pi )(r^{2})$
4
Isolate $(\pi )(r^{2})$ . To do this, divide both sides of the equation by the fraction or decimal you just calculated.

Example
$50={\frac {1}{3}}(\pi )(r^{2})$
${\frac {50}{\frac {1}{3}}}={\frac {{\frac {1}{3}}(\pi )(r^{2})}{\frac {1}{3}}}$
$150=(\pi )(r^{2})$
5
Divide both sides of the equation by $\pi$ . This will isolate the $r$ variable. For a more precise result, use a calculator. You can also round $\pi$ to 3.14.

Example
$150=(\pi )(r^{2})$
${\frac {150}{\pi }}={\frac {(\pi )(r^{2})}{\pi }}$
$47.7=r^{2}$
6
Take the square root of both sides. This will give you the radius of the circle.

Example
$47.7=r^{2}$
${\sqrt {47.7}}={\sqrt {r^{2}}}$
$6.91=r$
So, the radius of the circle is about 6.91 centimeters.

Practice Problems and Answers

Practice Problems to Calculate Radius of a Circle

Community Q&A

Question

How do I find the radius of a circle when I know the chord length?

Community Answer

It is possible to have quite a few circles, all with different radii, in which one could draw a chord of a given, fixed length. Hence, the chord length by itself cannot determine the radius of the circle.
Question

How do I find the radius of a circle when I know the arc length and the central angle?

Donagan

Top Answerer

Divide the central angle into 360°. Multiply the resulting number by the arc length. That gives you the circumference of the circle. Divide the circumference by pi. That's the diameter. Half of the diameter is the radius of the circle.
Question

How do I calculate the radius of a circle when no other values are known?

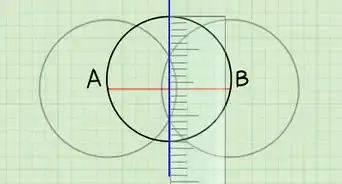
Community Answer

Technically you can't "calculate" the radius in such a situation. However, it is possible, by construction, to locate the center of such a circle, and then, simply by physically measuring, determine the radius. To do the construction, draw any two chords and construct their perpendicular bisectors; their point of intersection is the center of the circle. Then draw in any radius and measure it with a ruler. Not technically a "calculation."