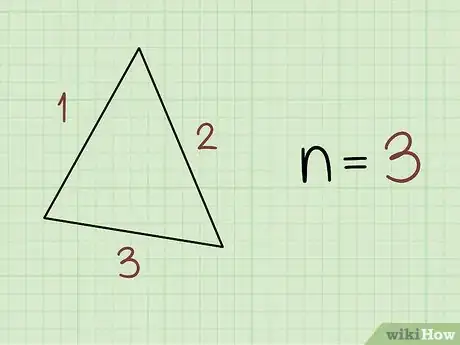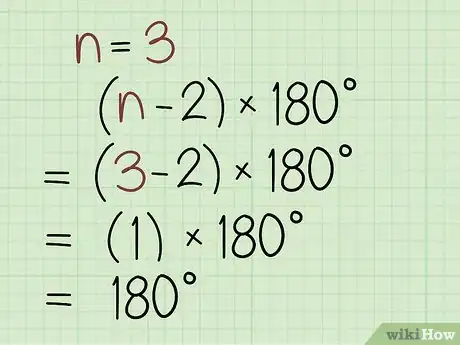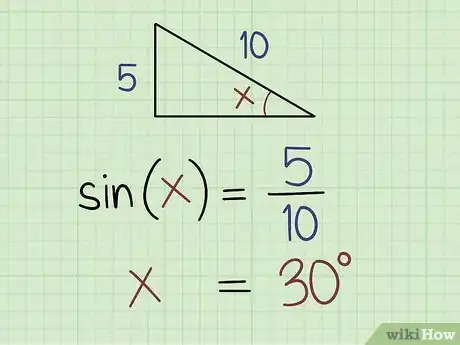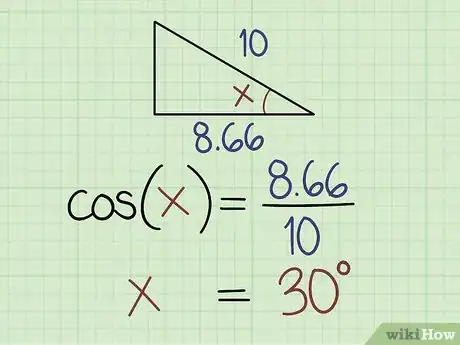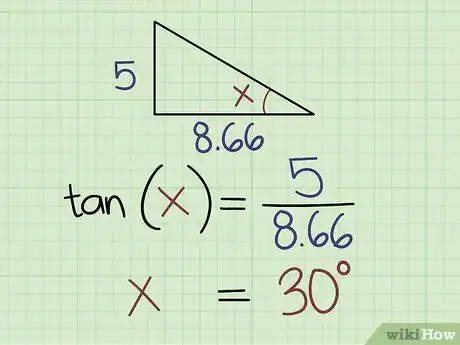How to Calculate Angles

Co-authored by Mario Banuelos, PhD and Sophia Latorre

In geometry, an angle is the space between 2 rays (or line segments) with the same endpoint (or vertex). The most common way to measure angles is in degrees, with a full circle measuring 360 degrees. You can calculate the measure of an angle in a polygon if you know the shape of the polygon and the measure of its other angles or, in the case of a right triangle, if you know the measures of two of its sides. Additionally, you can measure angles using a protractor or calculate an angle without a protractor using a graphing calculator. This is to allow you to calculate angles

Method 1

Method 1 of 2:

Calculating Interior Angles in a Polygon

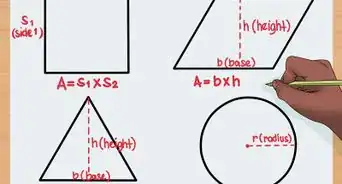
1
Count the number of sides in the polygon. In order to calculate the interior angles of a polygon, you need to first determine how many sides the polygon has. Note that a polygon has the same number of sides as it has angles.^{[1]
X
Research source}
- For instance, a triangle has 3 sides and 3 interior angles while a square has 4 sides and 4 interior angles.
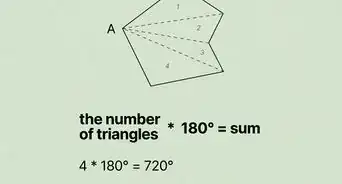
2
Find the total measure of all of the interior angles in the polygon. The formula for finding the total measure of all interior angles in a polygon is: (n – 2) x 180. In this case, n is the number of sides the polygon has. Some common polygon total angle measures are as follows:^{[2]
X
Research source}
- The angles in a triangle (a 3-sided polygon) total 180 degrees.
- The angles in a quadrilateral (a 4-sided polygon) total 360 degrees.
- The angles in a pentagon (a 5-sided polygon) total 540 degrees.
- The angles in a hexagon (a 6-sided polygon) total 720 degrees.
- The angles in an octagon (an 8-sided polygon) total 1080 degrees.
Advertisement
3
Divide the total measure of all of a regular polygon's angles by the number of its angles. A regular polygon is a polygon whose sides are all the same length and whose angles all have the same measure. For instance, the measure of each angle in an equilateral triangle is 180 ÷ 3, or 60 degrees, and the measure of each angle in a square is 360 ÷ 4, or 90 degrees.^{[3]
X
Research source}
- Equilateral triangles and squares are examples of regular polygons, while the Pentagon in Washington, D.C. is an example of a regular pentagon and a stop sign is an example of a regular octagon.
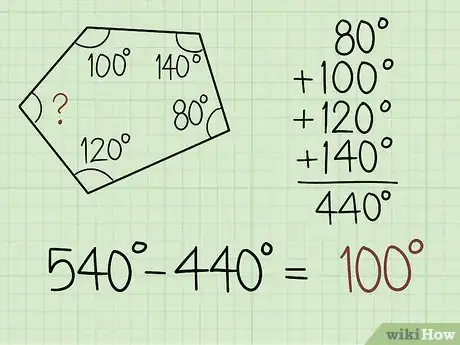
4
Subtract the sum of the known angles from the total measure of the angles for an irregular polygon. If your polygon doesn't have sides of the same length and angles of the same measure, all you need to do is add up all of the known angles in the polygon. Then, subtract that number from the total measure of all of the angles to find the missing angle.^{[4]
X
Research source}
- For example, if you know that 4 of the angles in a pentagon measure 80, 100, 120, and 140 degrees, add the numbers together to get a sum of 440. Then, subtract this sum from the total angle measure for a pentagon, which is 540 degrees: 540 – 440 = 100 degrees. So, the missing angle is 100 degrees.
Tip: Some polygons offer “cheats” to help you figure out the measure of the unknown angle. An isosceles triangle is a triangle with 2 sides of equal length and 2 angles of equal measure. A parallelogram is a quadrilateral with opposite sides of equal lengths and angles diagonally opposite each other of equal measure.

Method 2

Method 2 of 2:

Finding Angles in a Right Triangle

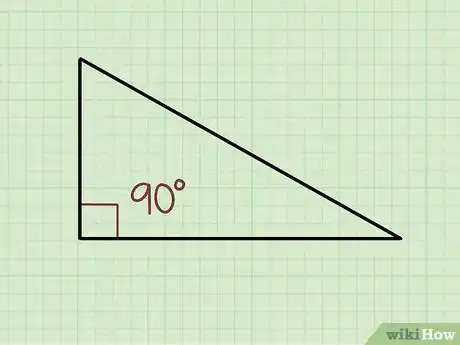
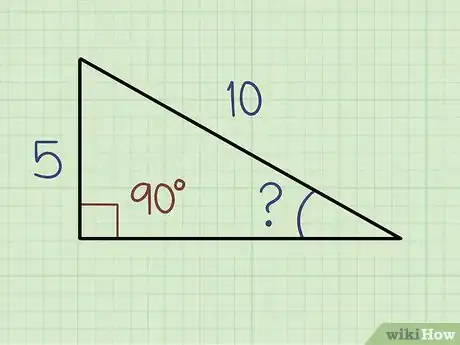
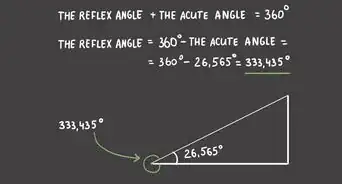
1
Remember that every right triangle has one angle equal to 90 degrees. By definition, a right triangle will always have one angle that's 90 degrees, even if it's not labeled as such. So, you will always know at least one angle and can use trigonometry to find out the other 2 angles.^{[5]
X
Research source}
2
Measure the length of 2 of the triangle's sides. The longest side of a triangle is called the “hypotenuse.” The “adjacent” side is adjacent (or next to) to the angle you're trying to determine.^{[6]
X
Research source} The “opposite” side is opposite to the angle you're trying to determine. Measure 2 of the sides so you can determine the measure of the remaining angles in the triangle.^{[7]
X
Expert Source

Mario Banuelos, PhD
Assistant Professor of Mathematics
Expert Interview. 19 January 2021.}

Tip: You can use a graphing calculator to solve your equations or find a table online that lists the values for various sine, cosine, and tangent functions.
3
Use the sine function if you know the length of the opposite side and the hypotenuse. Plug your values into the equation: sine (x) = opposite ÷ hypotenuse. Say that the length of the opposite side is 5 and the length of the hypotenuse is 10. Divide 5 by 10, which is equal to 0.5. Now you know that sine (x) = 0.5 which is the same as x = sine^-1 (0.5).^{[8]
X
Research source}
- If you have a graphing calculator, simply type 0.5 and press sine^-1. If you don't have a graphing calculator, use an online chart to find the value. Both will show that x = 30 degrees.
4
Use the cosine function if you know the length of the adjacent side and the hypotenuse. For this type of problem, use the equation: cosine (x) = adjacent ÷ hypotenuse. If the length of the adjacent side is 1.666 and the length of the hypotenuse is 2.0, divide 1.666 by 2, which is equal to 0.833. So, cosine (x) = 0.833 or x = cosine^-1 (0.833).^{[9]
X
Research source}
- Plug 0.833 into your graphing calculator and press cosine^-1. Alternatively, look up the value in a cosine chart. The answer is 33.6 degrees.
5
Use the tangent function if you know the length of the opposite side and the adjacent side. The equation for tangent functions is tangent (x) = opposite ÷ adjacent. Say you know the length of the opposite side is 75 and the length of the adjacent side is 100. Divide 75 by 100, which is 0.75. This means that tangent (x) = 0.75, which is the same as x = tangent^-1 (0.75).^{[10]
X
Research source}
- Find the value in a tangent chart or press 0.75 on your graphing calculator, then tangent^-1. This is equal to 36.9 degrees.

Expert Q&A
Did you know you can get expert answers for this article? Unlock expert answers by supporting wikiHow

Question

How do you find an angle?

Mario Banuelos, PhD
Assistant Professor of Mathematics
Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Mario Banuelos, PhD

Assistant Professor of Mathematics

Expert Answer

Support wikiHow by unlocking this expert answer.

To calculate angles, you can use side lengths and the trigonometric functions tangent, sine, and cosine.
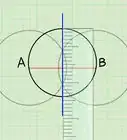
Question

How do I create a 90 degree corner by swinging an arch?

Donagan

Top Answerer

Pick a convenient point on a line to be the vertex of your 90° angle. Choose two points on the line, one on each side of the vertex and equidistant from the vertex. Use a compass to draw two arcs of the same diameter, each centered on one of those latter points. Draw a line connecting the vertex point with the intersecting point(s) of the arcs. That line describes a 90° angle with the first line.
Question

How do I find the interior angles of a hexagon without base or height or anything?

Donagan

Top Answerer

The sum of the six interior angles of a regular polygon is (n-2)(180°), where n is the number of sides. Therefore, in a hexagon the sum of the angles is (4)(180°) = 720°. All the angles are equal, so divide 720° by 6 to get 120°, the size of each interior angle.