How to Find the Center of a Circle

Co-authored by David Jia

Last Updated: March 26, 2023 References Approved

Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.

Things You Should Know

Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
Sketch two separate sets of overlapping circles to identify the exact center point.
Draw a square snugly around the circle. Sketch an "X" between all 4 corners of the square to find the circle's center.

Method 1

Method 1 of 3:

Drawing Crossed Lines

1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you're finding the center of an existing circle, then you don't need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store!^{[1]
  X
  Research source}
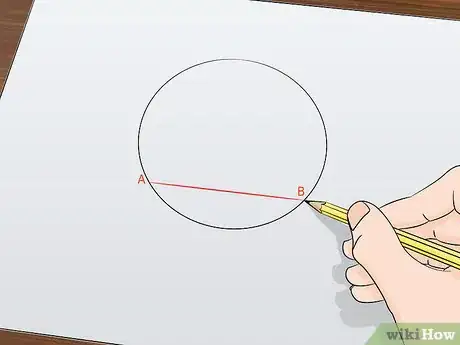
2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.^{[2]
X
Research source} Name the chord AB.
- Consider using a pencil to sketch your lines. This way, you can erase the marks once you've found the center. Draw with a light touch so that it'll be easier to erase.
Advertisement
3
Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.^{[3]
X
Research source}
4
Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
5
Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
6
Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.^{[4]
X
Research source} Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.

Method 2

Method 2 of 3:

Using Overlapping Circles

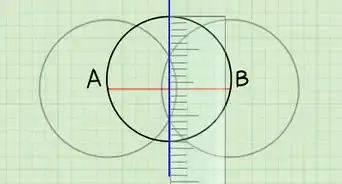
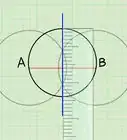
1
Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don't matter. Label the two points A and B.
2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
3
Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the "Venn diagram" space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
4
Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
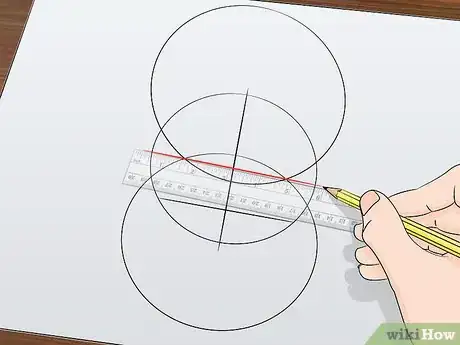
5
Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
6
Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
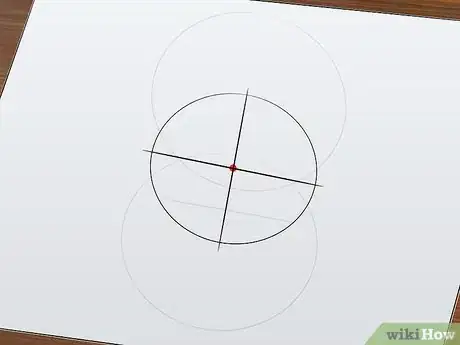
7
Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.

Method 3

Method 3 of 3:

Using a Straightedge and a Triangular Ruler

1
Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.^{[5]
X
Research source}
2
Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
3
Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle's center.
4
Check the accuracy of the center with a compass. The center should be on target as long as you didn't slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.

Practice Problems and Answers

Practice Problems and Answers to Find the Center of a Circle

Expert Q&A
Did you know you can get expert answers for this article? Unlock expert answers by supporting wikiHow

Question

How do you find the center of a circle if you're only given the equation?

David Jia
Academic Tutor
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

David Jia

Academic Tutor

Expert Answer

Support wikiHow by unlocking this expert answer.

The equation of a circle is (x-h)²+(y-k)²=r². The coordinates for the center of the circle are (h, k), so to find the center of the circle, solve for h and k.
Question

How do you find the center of the circle if you're only given the endpoints of the diameter?

David Jia
Academic Tutor
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

David Jia

Academic Tutor

Expert Answer

Support wikiHow by unlocking this expert answer.

If you're given two points that are the endpoints of the diameter of the circle, the midpoint of that line will be the center of the circle.
Question

In the first method, what do I do if the chords are of different lengths?

Community Answer

It's not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here's a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle's center.

Warnings

A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.

⧼thumbs_response⧽
Helpful 15 Not Helpful 8
In order to find the true center of a circle, you must use a geometric compass and a straightedge.

⧼thumbs_response⧽
Helpful 6 Not Helpful 4