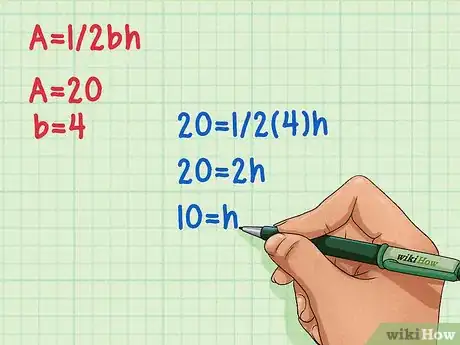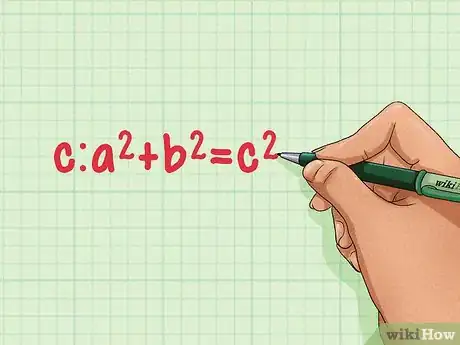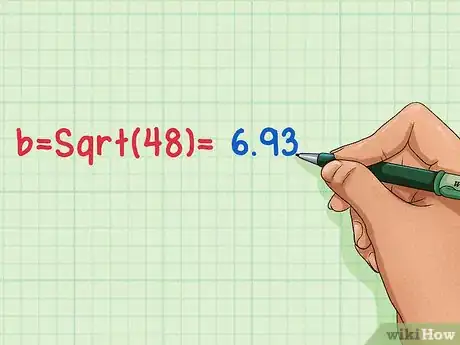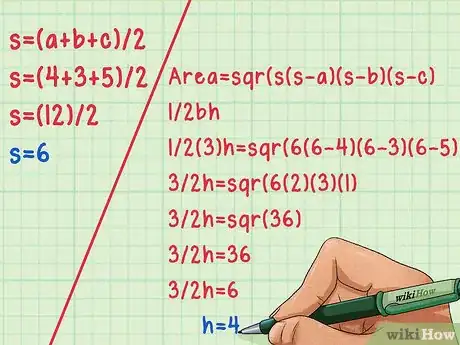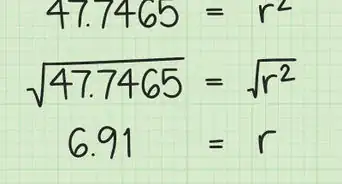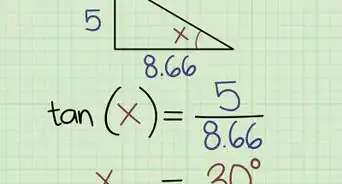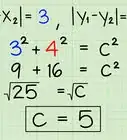This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
This article has been viewed 2,366,134 times.
To calculate the area of a triangle you need to know its height. To find the height follow these instructions. You must at least have a base to find the height.
Steps
Using Base and Area to Find Height
-
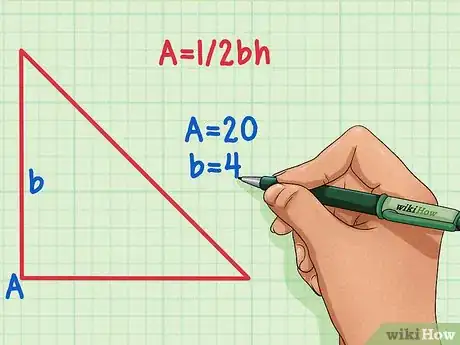
1Recall the formula for the area of a triangle. The formula for the area of a triangle isA=1/2bh.[1]
- A = Area of the triangle
- b = Length of the base of the triangle
- h = Height of the base of the triangle
-
2Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to "'b'".Any side of a triangle can be the base,regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom.
Example
If you know that the area of a triangle is 20, and one side is 4, then:
A = 20 and b = 4.Advertisement -
3Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle!
Example
20 = 1/2(4)h Plug the numbers into the equation.
20 = 2h Multiply 4 by 1/2.
10 = h Divide by 2 to find the value for height.
Finding an Equilateral Triangle's Height
-
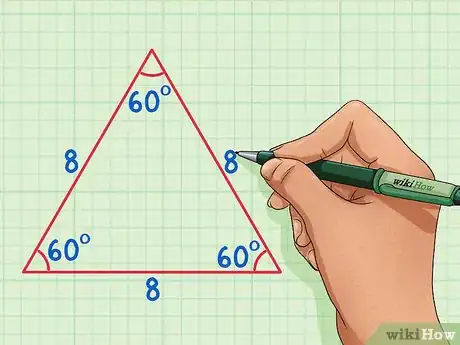
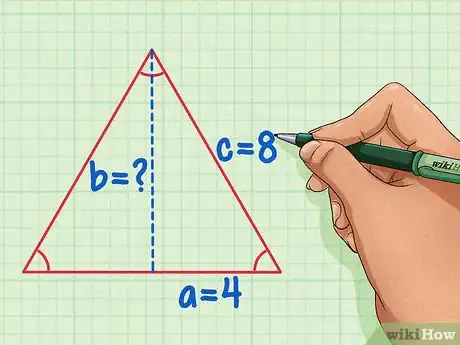
1Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If youcut an equilateral triangle in half, you will end up with two congruent right triangles.[2]
- In this example, we will be using an equilateral triangle with side lengths of 8.
-
2Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c:a2 + b2 = c2.We can use this theorem to find the height of our equilateral triangle![3]
-
3Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve.
- Using our example equilateral triangle with sides of 8, c = 8 and a = 4.
-
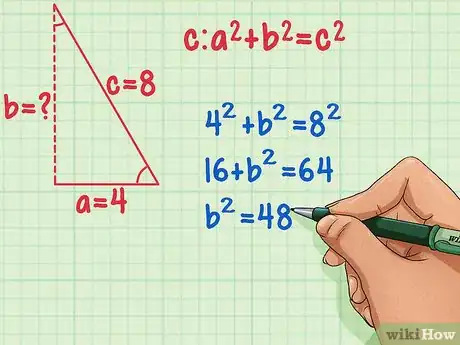
4Plug the values into the Pythagorean Theorem and solve for b2.[4] First square c and a by multiplying each number by itself. Then subtract a2 from c2.
Example
42 + b2 = 82 Plug in the values for a and c.
16 + b2 = 64 Square a and c.
b2 = 48 Subtract a2 from c2. -
5Find the square root of b2 to get the height of your triangle! Use the square root function on your calculator to find Sqrt(2. The answer is the height of your equilateral triangle!
- b = Sqrt (48) = 6.93
Determining Height With Angles and Sides
-
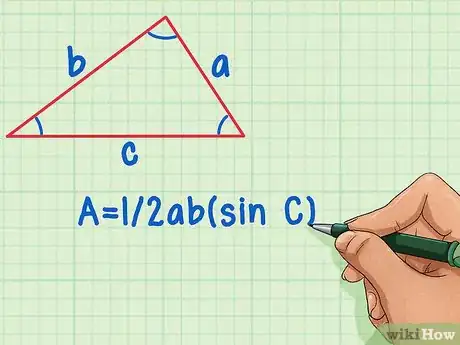
1Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We'll call the sides of the triangle a, b, and c, and the angles, A, B, and C.
- If you have all three sides, you'll use Heron's formula, and the formula for the area of a triangle.
- If you have two sides and an angle, you'll use the formula for the area given two angles and a side. A = 1/2ab(sin C).[5]
- If you have all three sides, you'll use
-
2Use Heron's formula if you have all three sides. Heron's formula has two parts. First, you must find the variables, which is equal to half of the perimeter of the triangle.This is done with this formula:s = (a+b+c)/2.[6]
Heron's Formula Example
For a triangle with sides a = 4, b = 3, and c = 5:
s = (4+3+5)/2
s = (12)/2
s = 6
Then use the second part of Heron's formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).
Solve for h. For our example triangle this looks like:
1/2(3)h = sqr(6(6-4)(6-3)(6-5).
3/2h = sqr(6(2)(3)(1)
3/2h = sqr(36)
Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.
Therefore, height is equal to 4, using side b as the base. -
3Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified toh = a(sin C), thereby eliminating one of the side variables.[7] Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side).
Finding Height with 1 Side and 1 Angle Example
For example, with a = 3, and C = 40 degrees, the equation looks like this:
h = 3(sin 40)
Use your calculator to finish the equation, which makes h roughly 1.928.
Practice Problems and Answers
Community Q&A
-
QuestionHow do I find the area of an equilateral triangle when only the height is given?
 Community AnswerH = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find.
Community AnswerH = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find. -
QuestionHow do I calculate the height of a right triangle, given only the length of the base and the interior angle at the base?
 DonaganTop AnswererLook up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base.
DonaganTop AnswererLook up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base. -
QuestionHow do I determine the height of a triangle when I know the length of all three sides?
 Community AnswerYou already know the base, so calculate the area by Heron's formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
Community AnswerYou already know the base, so calculate the area by Heron's formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
References
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
- ↑ http://www.mathsisfun.com/definitions/equilateral-triangle.html
- ↑ http://www.mathsisfun.com/pythagoras.html
- ↑ http://mathcentral.uregina.ca/qq/database/qq.09.05/kelsey1.html
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
- ↑ http://www.mathsisfun.com/geometry/herons-formula.html
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
About This Article
If you know the base and area of the triangle, you can divide the base by 2, then divide that by the area to find the height. To find the height of an equilateral triangle, use the Pythagorean Theorem, a^2 + b^2 = c^2. Cut the triangle in half down the middle, so that c is equal to the original side length, a equals half of the original side length, and b is the height. Plug a and c into the equation, squaring both of them. Then subtract a^2 from c^2 and take the square root of the difference to find the height. If you want to learn how to calculate the area if you only know the angles and sides, keep reading!