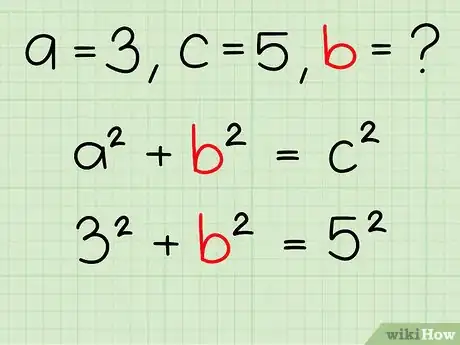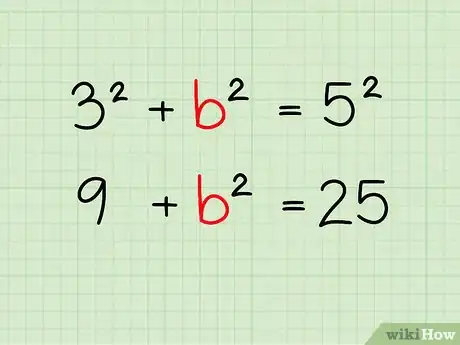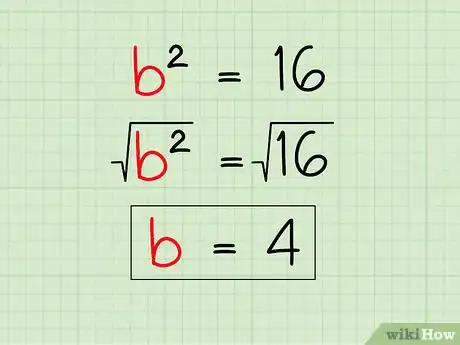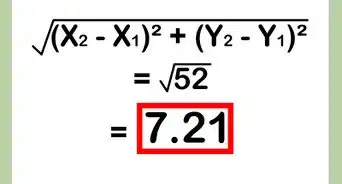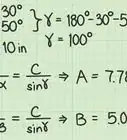wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 67 people, some anonymous, worked to edit and improve it over time.
There are 10 references cited in this article, which can be found at the bottom of the page.
wikiHow marks an article as reader-approved once it receives enough positive feedback. In this case, several readers have written to tell us that this article was helpful to them, earning it our reader-approved status.
This article has been viewed 401,200 times.
Learn more...
The Pythagorean Theorem describes the lengths of the sides of a right triangle in a way that is so elegant and practical that the theorem is still widely used today. The theorem states that for any right triangle, the sum of the squares of the non-hypotenuse sides is equal to the square of the hypotenuse. In other words, for a right triangle with perpendicular sides of length a and b and hypotenuse of length c, a2 + b2 = c2. The Pythagorean Theorem is one of the fundamental pillars of basic geometry, having countless practical applications - using the theorem, for instance, it's easy to find the distance between two points on a coordinate plane.
Steps
Finding the Sides of a Right Triangle
-
1Ensure that your triangle is a right triangle. The Pythagorean Theorem is applicable only to right triangles, so, before proceeding, it's important to make sure your triangle fits the definition of a right triangle. Luckily, there is only one qualifying factor - to be a right triangle, your triangle must contain one angle of exactly 90 degrees.[1]
- As a form of visual shorthand, right angles are often marked with a small square, rather than a rounded "curve", to identify them as such. Look for this special mark in one of the corners of your triangle.
-
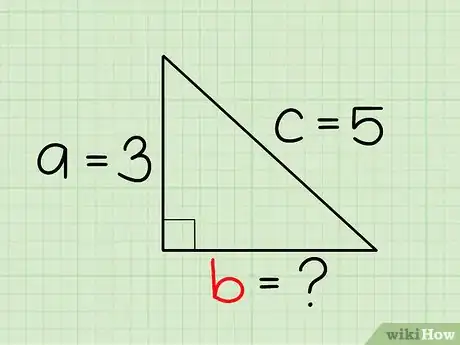
2Assign the variables a, b, and c to the sides of your triangle. In the Pythagorean Theorem, the variables a and b refer to the sides that meet in a right angle, while the variable c refers to the hypotenuse - the longest side which is always opposite the right angle. So, to begin, assign the shorter sides of your triangle the variables a and b (it doesn't matter which side is labeled 'a' or 'b'), and assign the hypotenuse the variable c.[2]Advertisement
-
3Determine which side(s) of the triangle you are solving for. The Pythagorean Theorem allows mathematicians to find the length of any one of a right triangle's sides as long as they know the lengths of the other two sides. Determine which of your sides has an unknown length - a, b, and/or c. If the length of only one of your sides is unknown, you're ready to proceed.[3]
- Let's say, for example, that we know that our hypotenuse has a length of 5 and one of the other sides has a length of 3, but we're not sure what the length of the third side is. In this case, we know we're solving for the length of the third side, and, because we know the lengths of the other two, we're ready to go! We'll return to this example problem in the following steps.
- If the lengths of two of your sides are unknown, you'll need to determine the length of one more side to use the Pythagorean Theorem. Basic trigonometry functions can help you here if you know one of the non-right angles in the triangle.
-
4Plug your two known values into the equation. Insert your values for the lengths of the sides of your triangle into the equation a2 + b2 = c2. Remember that a and b are the non hypotenuse sides, while c is the hypotenuse.[4]
- In our example, we know the length of one side and the hypotenuse (3 & 5), so we would write our equation as 3² + b² = 5²
-
5Calculate the squares. To solve your equation, begin by taking the square of each of your known sides. Alternatively, if you find it easier, you may leave your side lengths in the exponent form, then square them later.[5]
- In our example, we would square 3 and 5 to get 9 and 25, respectively. We can rewrite our equation as 9 + b² = 25.
-
6Isolate your unknown variable on one side of the equals sign. If necessary, use basic algebra operations to get your unknown variable on one side of the equals sign and your two squares on the other side of the equals sign. If you're solving for the hypotenuse, c will already be isolated, so you won't need to do anything to isolate it.[6]
- In our example, our current equation is 9 + b² = 25. To isolate b², let's subtract 9 from both sides of the equation. This leaves us with b² = 16.
-
7Take the square root of both sides of the equation. You should now be left with one variable squared on one side of the equation and a number on the other side. Simply take the square root of both sides to find the length of your unknown side.[7]
- In our example, b² = 16, taking the square root of both sides gives us b = 4. Thus, we can say that the length of the unknown side of our triangle is 4.
-
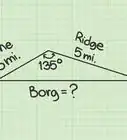
8Use the Pythagorean Theorem to find the sides of real-world right triangles. The reason that the Pythagorean Theorem is so widely used today is that it's applicable in countless practical situations. Learn to recognize right triangles in real life - in any situation where two straight objects or lines meet at a right angle and a third line or object stretches diagonally across from the right angle, you can use the Pythagorean Theorem to find the length of one of the sides, given the length of the other two.[8]
- Let's try real-world example that's a little more difficult. A ladder is leaning against a building. The base of the ladder is 5 meters (16.4 ft) from the bottom of the wall. The ladder reaches 20 meters (65.6 ft) up the wall of the building. How long is the ladder?
- "5 meters (16.4 ft) from the bottom of wall” and "20 meters (65.6 ft) up the wall” clue us into the lengths of the sides of our triangle. Since the wall and the ground (presumably) meet at a right angle and the ladder leans diagonally against the wall, we can think of this arrangement as a right triangle with sides of length a = 5 and b = 20. The length of the ladder is the hypotenuse, so c is our unknown. Let's use the Pythagorean Theorem:
- a² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- sqrt(425) = c
- c = 20.6 . The approximate length of the ladder is 20.6 meters (67.6 ft).
- "5 meters (16.4 ft) from the bottom of wall” and "20 meters (65.6 ft) up the wall” clue us into the lengths of the sides of our triangle. Since the wall and the ground (presumably) meet at a right angle and the ladder leans diagonally against the wall, we can think of this arrangement as a right triangle with sides of length a = 5 and b = 20. The length of the ladder is the hypotenuse, so c is our unknown. Let's use the Pythagorean Theorem:
- Let's try real-world example that's a little more difficult. A ladder is leaning against a building. The base of the ladder is 5 meters (16.4 ft) from the bottom of the wall. The ladder reaches 20 meters (65.6 ft) up the wall of the building. How long is the ladder?
Calculating the Distance Between Two Points in an X-Y Plane
-
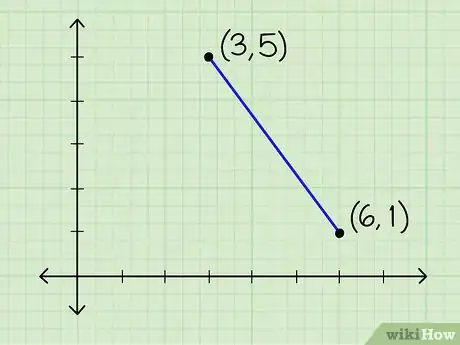
1Define two points in the X-Y plane. The Pythagorean Theorem can easily be used to calculate the straight-line distance between two points in the X-Y plane. All you need to know are the x and y coordinates of any two points. Usually, these coordinates are written as ordered pairs in the form (x, y).[9]
- To find the distance between these two points, we will treat each point as one of the non-right angle corners of a right triangle. By doing this, it's easy to find the length of the a and b sides, then calculate c, the hypotenuse, which is the distance between the two points.
-
2Plot your two points on a graph. In a typical X-Y plane, for each point (x,y), x gives a coordinate on the horizontal axis and y gives a coordinate on the vertical axis. You can find the distance between the two points without plotting them on a graph, but doing so gives you a visual reference that you can use to ensure your answer makes sense.[10]
-
3Find the lengths of the non-hypotenuse sides of your triangle. Using your two points as the corners of the triangle adjacent to the hypotenuse, find the lengths of the a and b sides of the triangle. You can do this visually on the graph, or by using the formulas |x1 - x2| for the horizontal side and |y1 - y2| for the vertical side, where (x1,y1) is your first point and (x2,y2) is your second.[11]
- Let's say our two points are (6,1) and (3,5). The side length of the horizontal side of our triangle is:
- |x1 - x2|
- |3 - 6|
- | -3 | = 3
- The length of the vertical side is:
- |y1 - y2|
- |1 - 5|
- | -4 | = 4
- So, we can say that in our right triangle, side a = 3 and side b = 4.
- Let's say our two points are (6,1) and (3,5). The side length of the horizontal side of our triangle is:
-
4Use the Pythagorean Theorem to solve for the hypotenuse. The distance between your two points is the hypotenuse of the triangle whose two sides you've just defined. Use the Pythagorean Theorem as you normally would to find the hypotenuse, setting a as the length of your first side and b as the length of the second.[12]
- In our example using points (3,5) and (6,1), our side lengths are 3 and 4, so we would find the hypotenuse as follows:
- (3)²+(4)²= c²
- c= sqrt(9+16)
- c= sqrt(25)
- c= 5. The distance between (3,5) and (6,1) is 5.
- In our example using points (3,5) and (6,1), our side lengths are 3 and 4, so we would find the hypotenuse as follows:
Community Q&A
-
QuestionWhat is the technical use of Pythagorean Theorem?
 DonaganTop AnswererThe Pythagorean Theorem allows you to find the length of one side of a right triangle when you know the lengths of the other two sides.
DonaganTop AnswererThe Pythagorean Theorem allows you to find the length of one side of a right triangle when you know the lengths of the other two sides. -
QuestionHow can I find the slope dimension of a staircase?
 DonaganTop AnswererMeasure the horizontal and vertical distances from the top stair to the bottom stair, and use those two distances as "a" and "b" in the formula.
DonaganTop AnswererMeasure the horizontal and vertical distances from the top stair to the bottom stair, and use those two distances as "a" and "b" in the formula. -
QuestionHow do I find the sides of a right triangle when I only have the length of the hypotenuse?
 Community AnswerYou can find the side with the help of an angle inside the triangle. Using sin of the angle gives you the opposite side divided by the hypotenuse or cos of the angle gives you the adjacent side divided with the hypotenuse.
Community AnswerYou can find the side with the help of an angle inside the triangle. Using sin of the angle gives you the opposite side divided by the hypotenuse or cos of the angle gives you the adjacent side divided with the hypotenuse.
References
- ↑ https://www.mathwarehouse.com/geometry/triangles/how-to-use-the-pythagorean-theorem.php
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U07_L1_T4_text_final.html
- ↑ https://www.mathsisfun.com/pythagoras.html
- ↑ https://www.mathsisfun.com/pythagoras.html
- ↑ https://www.mathplanet.com/education/pre-algebra/right-triangles-and-algebra/the-pythagorean-theorem
- ↑ https://www.cuemath.com/geometry/pythagoras-theorem/
- ↑ https://www.cuemath.com/geometry/pythagoras-theorem/
- ↑ https://sciencing.com/real-life-uses-pythagorean-theorem-8247514.html
- ↑ https://courses.lumenlearning.com/waymakercollegealgebra/chapter/distance-in-the-plane/
About This Article
To use the Pythagorean Theorem on a triangle with a 90-degree angle, label the shorter sides of the triangle a and b, and the longer side opposite of the right angle should be labelled c. As long as you know the length of two of the sides, you can solve for the third side by using the formula a squared plus b squared equals c squared. Place your known values into the equation and solve for the unknown variable, then take the square root of both sides of the equation to get the result. If you want to use the Pythagorean Theorem to find the distance between 2 points, keep reading the article!