Other Hypothesis Tests

A t-test is any statistical hypothesis test in which the test statistic follows a Student's t-distribution if the null hypothesis is supported.

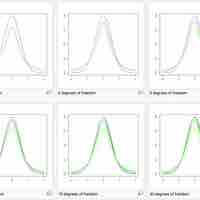
Student's $t$-distribution arises in estimation problems where the goal is to estimate an unknown parameter when the data are observed with additive errors.

Assumptions of a $t$-test depend on the population being studied and on how the data are sampled.

The $t$-test is the most powerful parametric test for calculating the significance of a small sample mean.

Two-sample t-tests for a difference in mean involve independent samples, paired samples, and overlapping samples.

Paired-samples $t$-tests typically consist of a sample of matched pairs of similar units, or one group of units that has been tested twice.

The following is a discussion on explicit expressions that can be used to carry out various $t$-tests.

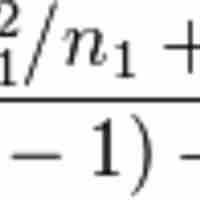
The following is a discussion on explicit expressions that can be used to carry out various t-tests.

Hotelling's $T$-square statistic allows for the testing of hypotheses on multiple (often correlated) measures within the same sample.

When the normality assumption does not hold, a nonparametric alternative to the $t$-test can often have better statistical power.

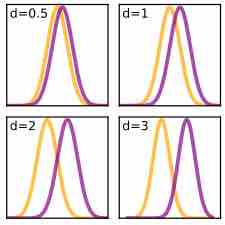
Cohen's $d$ is a method of estimating effect size in a $t$-test based on means or distances between/among means.

The multinomial experiment is the test of the null hypothesis that the parameters of a multinomial distribution equal specified values.

The chi-square test is used to determine if a distribution of observed frequencies differs from the theoretical expected frequencies.

Fisher's exact test is preferable to a chi-square test when sample sizes are small, or the data are very unequally distributed.

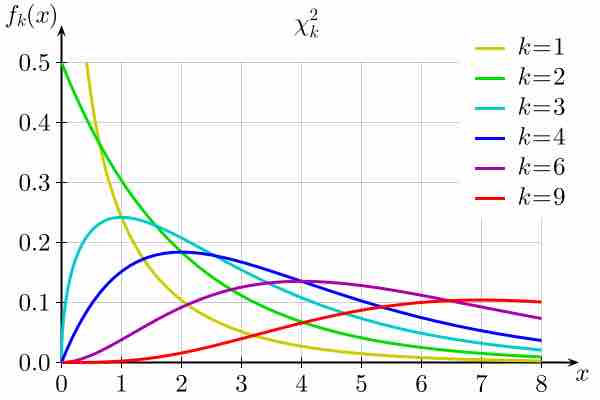
The goodness of fit test determines whether the data "fit" a particular distribution or not.

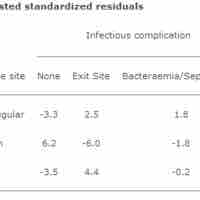
The chi-square test of association allows us to evaluate associations (or correlations) between categorical data.

The Chi-square test for goodness of fit compares the expected and observed values to determine how well an experimenter's predictions fit the data.

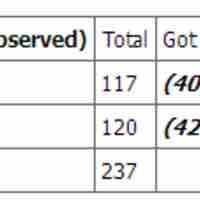
The chi-square test for independence is used to determine the relationship between two variables of a sample.

"Ranking" refers to the data transformation in which numerical or ordinal values are replaced by their rank when the data are sorted.

The Mann–Whitney $U$-test is a non-parametric test of the null hypothesis that two populations are the same against an alternative hypothesis.

The Wilcoxon $t$-test assesses whether population mean ranks differ for two related samples, matched samples, or repeated measurements on a single sample.

The Kruskal–Wallis one-way analysis of variance by ranks is a non-parametric method for testing whether samples originate from the same distribution.

Distribution-free tests are hypothesis tests that make no assumptions about the probability distributions of the variables being assessed.

The sign test can be used to test the hypothesis that there is "no difference in medians" between the continuous distributions of two random variables.

Two notable nonparametric methods of making inferences about single populations are bootstrapping and the Anderson–Darling test.

Nonparametric independent samples tests include Spearman's and the Kendall tau rank correlation coefficients, the Kruskal–Wallis ANOVA, and the runs test.

McNemar's test is applied to $2 \times 2$ contingency tables with matched pairs of subjects to determine whether the row and column marginal frequencies are equal.

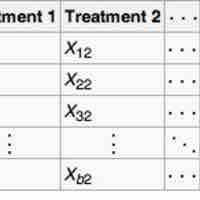
Nonparametric methods using randomized block design include Cochran's $Q$ test and Friedman's test.

A rank correlation is any of several statistics that measure the relationship between rankings.