The following is a discussion on explicit expressions that can be used to carry out various t-tests. In each case, the formula for a test statistic that either exactly follows or closely approximates a t-distribution under the null hypothesis is given. Also, the appropriate degrees of freedom are given in each case. Each of these statistics can be used to carry out either a one-tailed test or a two-tailed test.
Once a t-value is determined, a p-value can be found using a table of values from Student's t-distribution. If the calculated p-value is below the threshold chosen for statistical significance (usually the 0.10, the 0.05, or 0.01 level), then the null hypothesis is rejected in favor of the alternative hypothesis.
Independent Two-Sample T-Test
Equal Sample Sizes, Equal Variance
This test is only used when both:
- the two sample sizes (that is, the number, n, of participants of each group) are equal; and
- it can be assumed that the two distributions have the same variance.
Violations of these assumptions are discussed below. The t-statistic to test whether the means are different can be calculated as follows:
where
Here,
For significance testing, the degrees of freedom for this test is 2n − 2 where n is the number of participants in each group.
Unequal Sample Sizes, Equal Variance
This test is used only when it can be assumed that the two distributions have the same variance. The t-statistic to test whether the means are different can be calculated as follows:
where .
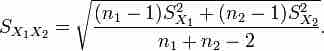
Pooled Variance
This is the formula for a pooled variance in a two-sample t-test with unequal sample size but equal variances.
Unequal (or Equal) Sample Sizes, Unequal Variances
This test, also known as Welch's t-test, is used only when the two population variances are assumed to be different (the two sample sizes may or may not be equal) and hence must be estimated separately. The t-statistic to test whether the population means are different is calculated as:
where .
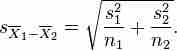
Unpooled Variance
This is the formula for a pooled variance in a two-sample t-test with unequal or equal sample sizes but unequal variances.
Here s2 is the unbiased estimator of the variance of the two samples, ni = number of participants in group i, i=1 or 2. Note that in this case
.
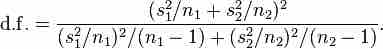
Welch–Satterthwaite Equation
This is the formula for calculating the degrees of freedom in Welsh's t-test.
This is known as the Welch–Satterthwaite equation. The true distribution of the test statistic actually depends (slightly) on the two unknown population variances.