Comparing Three or More Populations: Randomized Block Design

Cochran's $Q$ Test

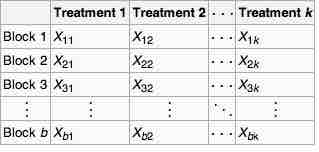
In the analysis of two-way randomized block designs, where the response variable can take only two possible outcomes (coded as $0$ and $1$), Cochran's $Q$ test is a non-parametric statistical test to verify if $k$ treatments have identical effects. Cochran's $Q$ test assumes that there are $k > 2$ experimental treatments and that the observations are arranged in $b$ blocks; that is:

Cochran's $Q$

Cochran's $Q$ test assumes that there are $k > 2$ experimental treatments and that the observations are arranged in $b$ blocks.

Cochran's $Q$ test is:

$H_0$: The treatments are equally effective.

$H_a$: There is a difference in effectiveness among treatments.

The Cochran's $Q$ test statistic is:

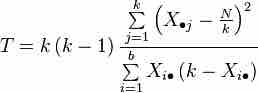
Cochran's $Q$ Test Statistic

This is the equation for Cochran's $Q$ test statistic, where

where

• $k$ is the number of treatments
• X• j is the column total for the j^th treatment
• b is the number of blocks
• X_i • is the row total for the i^th block
• N is the grand total

For significance level $\alpha$, the critical region is:

$T>{ X }_{ 1-\alpha ,k-1 }^{ 2 }$

where ${ X }_{ 1-\alpha ,k-1 }$ is the $(1-\alpha)$-quantile of the chi-squared distribution with $k-1$ degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the Cochran test rejects the null hypothesis of equally effective treatments, pairwise multiple comparisons can be made by applying Cochran's $Q$ test on the two treatments of interest.

Cochran's $Q$ test is based on the following assumptions:

1. A large sample approximation; in particular, it assumes that $b$ is "large."
2. The blocks were randomly selected from the population of all possible blocks.
3. The outcomes of the treatments can be coded as binary responses (i.e., a $0$ or $1$) in a way that is common to all treatments within each block.

The Friedman Test

The Friedman test is a non-parametric statistical test developed by the U.S. economist Milton Friedman. Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts. The procedure involves ranking each row (or block) together, then considering the values of ranks by columns.

Examples of use could include:

• $n$ wine judges each rate $k$ different wines. Are any wines ranked consistently higher or lower than the others?
• $n$ welders each use $k$ welding torches, and the ensuing welds were rated on quality. Do any of the torches produce consistently better or worse welds?

Method

1. Given data $\{ x_{ij} \} _{nxk}$, that is, a matrix with $n$ rows (the blocks), $k$ columns (the treatments) and a single observation at the intersection of each block and treatment, calculate the ranks within each block. If there are tied values, assign to each tied value the average of the ranks that would have been assigned without ties. Replace the data with a new matrix $\{ r_{ij} \} _{nxk}$ where the entry $r_{ij}$ is the rank of $x_{ij}$ within block$r_{ij}$ _i.

2. Find the values:

$\displaystyle{\bar{r}_{\cdot j} = \frac{1}{n} \sum_{i=1}^n r_{ij}\\ \bar{r} = \frac{1}{nk} \sum_{i=1}^n \sum_{j=1}^k r_{ij}\\ SS_t=n\sum_{j=1}^k(\bar{r}_{\cdot j}-\bar{r})^2\\ SS_e = \frac{1}{n(k-1)} \sum_{i=1}^n \sum_{j=1}^k (r_{ij} - \bar{r})^2}$

3. The test statistic is given by $Q=\frac { { SS }_{ t } }{ { SS }_{ e } }$. Note that the value of $Q$ as computed above does not need to be adjusted for tied values in the data.

4. Finally, when $n$ or $k$ is large (i.e. $n>15$ or $k > 4$), the probability distribution of $Q$ can be approximated by that of a chi-squared distribution. In this case the $p$-value is given by $P\left( { \chi }_{ k-1 }^{ 2 }\ge Q \right)$. If $n$ or $k$ is small, the approximation to chi-square becomes poor and the $p$-value should be obtained from tables of $Q$ specially prepared for the Friedman test. If the $p$-value is significant, appropriate post-hoc multiple comparisons tests would be performed.