Student's
If we take
The
History
The
Distribution of a Test Statistic
Student's
where:
-
$Z$ is normally distributed with expected value$0$ and variance$1$ - V has a chi-squared distribution with
$\nu$ degrees of freedom -
$Z$ and$V$ are independent
A different distribution is defined as that of the random variable defined, for a given constant
This random variable has a noncentral
Shape
The probability density function is symmetric; its overall shape resembles the bell shape of a normally distributed variable with mean
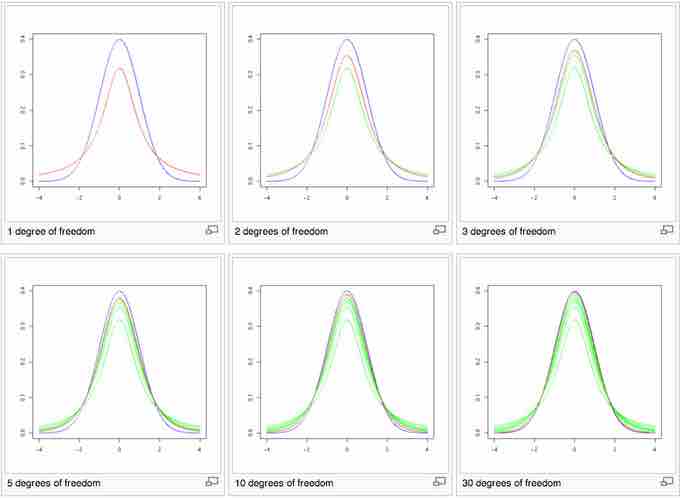
Shape of the $t$ -Distribution
These images show the density of the
Uses
Student's
Confidence intervals and hypothesis tests are two statistical procedures in which the quantiles of the sampling distribution of a particular statistic (e.g., the standard score) are required. In any situation where this statistic is a linear function of the data, divided by the usual estimate of the standard deviation, the resulting quantity can be rescaled and centered to follow Student's
A number of statistics can be shown to have