X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 10 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 297,265 times.
Learn more...
The Hungarian algorithm allows a "minimum matching" to be found. This can be used in instances where there are multiple quotes for a group of activities and each activity must be done by a different person, to find the minimum cost to complete all of the activities.
Steps
-
1
-
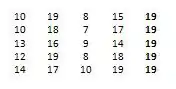
2Ensure that the matrix is square by the addition of dummy rows/columns if necessary. Conventionally, each element in the dummy row/column is the same as the largest number in the matrix.Advertisement
-
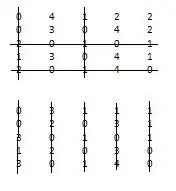
3Reduce the rows by subtracting the minimum value of each row from that row.
-
4
-
5
-
6
-
7
-
8
-
9
-
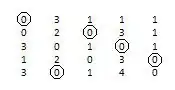
10Apply the matching to the original matrix, disregarding dummy rows. This shows who should do which activity, and adding the costs will give the total minimum cost.
Advertisement
Community Q&A
-
QuestionHow do the Dijkstra and Floyd algorithms differ?
 Community AnswerYou can use the Dijkstra algorithm to compute the shortest path from the source node to any other node. You can use the Floyd-Warshall algorithm to compute the shortest path from any node to any node. Don't use Dijkstra if there are arcs with negative weight. If there is a negative cycle in your graph, you cannot use a polynomial algorithm.
Community AnswerYou can use the Dijkstra algorithm to compute the shortest path from the source node to any other node. You can use the Floyd-Warshall algorithm to compute the shortest path from any node to any node. Don't use Dijkstra if there are arcs with negative weight. If there is a negative cycle in your graph, you cannot use a polynomial algorithm. -
QuestionHow is the Hungarian method applied for obtaining a solution if the matrix is a rectangle?
 Community AnswerYou would first add "dummy" row(s) or column(s) to make it square, with the "dummy" value being the highest value from that column or row, respectively.
Community AnswerYou would first add "dummy" row(s) or column(s) to make it square, with the "dummy" value being the highest value from that column or row, respectively. -
QuestionCan the column reduction be done first and row reduction second?
 Community AnswerYes, it does not matter which reduction you do first. Doing row reduction first will give you a different final matrix, but the optimal solution obtained from that matrix will be the same as you get by doing the column reduction first. Furthermore, doing the row reduction first can sometimes reduce the number of steps required to get the optimal solution.
Community AnswerYes, it does not matter which reduction you do first. Doing row reduction first will give you a different final matrix, but the optimal solution obtained from that matrix will be the same as you get by doing the column reduction first. Furthermore, doing the row reduction first can sometimes reduce the number of steps required to get the optimal solution.
Advertisement
Things You'll Need
- Paper
- Pen/pencil
About This Article
Advertisement