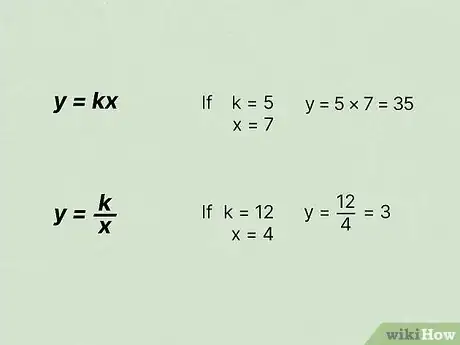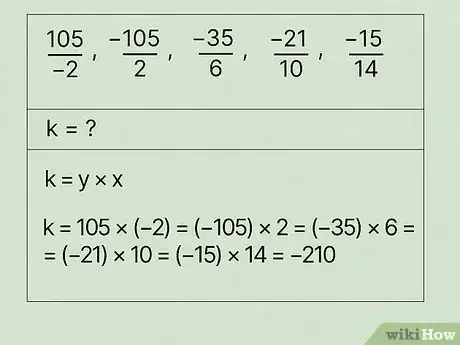Finding the Constant of Proportionality: Definition, Examples, and Practice Problems

Last Updated: October 25, 2022 References

The constant of proportionality tells you how much two sets of variables change. But how do you find it? You can figure it out by using a graph or an equation, and it's pretty simple to master. It's also something that you'll find you use all the time in real life, whether you're trying to calculate a discount at a store or figure out if you have enough gas in your car to make it to the next gas station. Read on to learn everything you need to know about the constant of proportionality, then try your hand at the practice problems. You've got this!

Things You Should Know

Find the constant of proportionality using the equation $k={\frac {y}{x}}$ when ratios are directly proportional (both increase at the same rate).
Find the constant of proportionality using the equation $k=yx$ when ratios are inversely proportional (one increases as the other decreases at the same rate).
Use the constant of proportionality to determine what value $y$ will be at any value of $x$ so you can graph the coordinates.

Section 1 of 6:

What is the constant of proportionality?

The constant of proportionality is the rate at which proportional variables change. When two variables are proportional, that means they both change at the same rate. If you plot them on a graph, you can draw a straight line between all of the points that goes through the origin of the graph. The constant of proportionality is the slope of that line.^{[1]
X
Research source}
- Graphed coordinates $(x,y)$ can also be written as a ratio $y:x$ or a fraction ${\frac {y}{x}}$ .
- You can also think of $x$ as the independent variable and $y$ as the dependent variable, since $y$ changes in relation to the change in $x$ .
- The constant of proportionality can never be $0$ .^{[2]
  X
  Research source}

Section 2 of 6:

Types of Proportionality

1
Direct proportionality: If two variables both increase at the same rate, they have a direct proportional relationship. Direct proportionality is represented by the equation $y=kx$ $y=kx$ where $k$ $k$ is the constant of proportionality.^{[3]
X
Research source}
- The same equation can also be written $k={\frac {y}{x}}$ . Use this version if you're trying to find the constant of proportionality and already have the values for the two variables.
- The formula $d=rt$ (distance = rate x time), which you might recognize from science class, is another version of the equation for the constant of proportionality.^{[4]
  X
  Research source}
2
Inverse proportionality: Ratios are inversely proportional if one amount decreases at the same rate that the other increases. Inverse proportionality is represented by the equation $y={\frac {k}{x}}$ $y={\frac {k}{x}}$ where $k$ $k$ is the constant of proportionality.^{[5]
X
Research source}
- The same equation can also be written $k=yx$ . Use this version to find the constant of proportionality when you already have the values for the other two variables.

Section 3 of 6:

Finding the Constant of Proportionality with Ratios

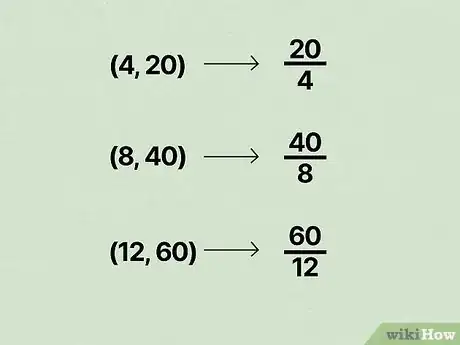
1
Set up each ratio as a fraction. In a ratio, the first number is the denominator of the fraction and the second number is the numerator. On a graph, the $x$ $x$ coordinate of any point is the denominator, while the $y$ $y$ coordinate is the numerator.^{[6]
X
Research source}
- For example, the ordered pairs $(4,20)$ , $(8,40)$ , and $(12,60)$ are the same as the ratios $20:4$ , $40:8$ , and $60:12$ . As fractions, they are ${\frac {20}{4}}$ , ${\frac {40}{8}}$ , and ${\frac {60}{12}}$ .
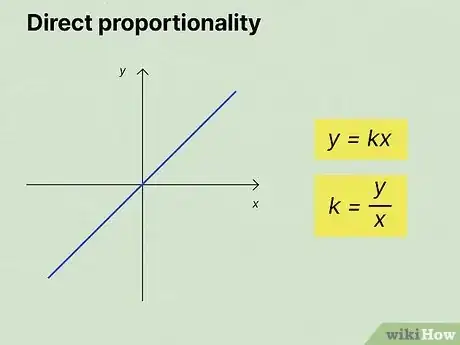
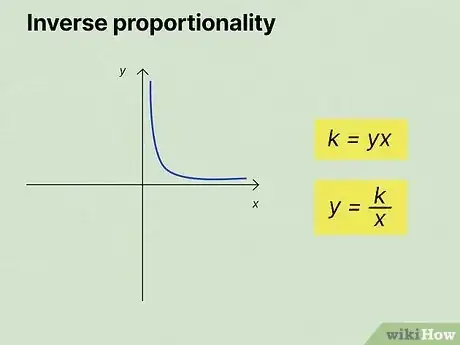
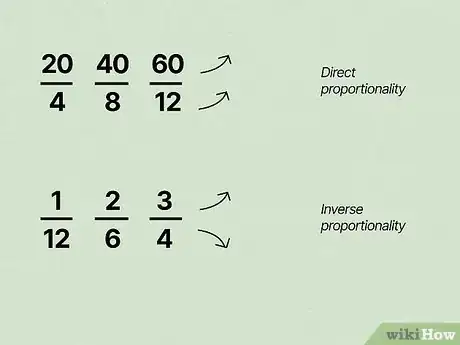
2
Determine whether you're looking at direct or inverse proportionality. Look at the numbers in the set of ratios you've been given. If they all increase, they're directly proportional. On the other hand, if one set of values increases and the other set of values decreases, you've got inverse proportionality.
- For example, look at the set ${\frac {20}{4}}$ , ${\frac {40}{8}}$ , and ${\frac {60}{12}}$ . In each ratio, the values of the numerator and the denominator both increase, so you're looking at direct proportionality.
- What if you had ${\frac {1}{12}}$ , ${\frac {2}{6}}$ , and ${\frac {3}{4}}$ ? The values of the denominator decrease as the values of the numerator increase, so you're looking at inverse proportionality.
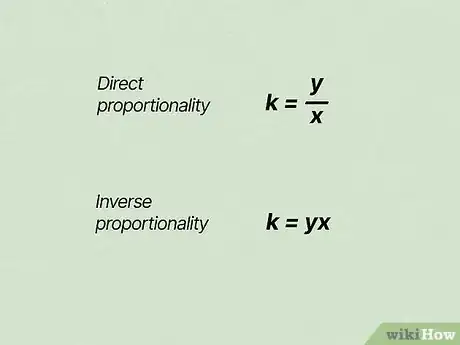
3
Plug the values from one of the ratios into the proper equation. If the ratios have direct proportionality, use the equation $k={\frac {y}{x}}$ $k={\frac {y}{x}}$ . For inverse proportionality, use the equation $k=yx$ $k=yx$ .^{[7]
X
Research source}
- To continue from the previous example, take the first ratio of ${\frac {20}{4}}$ . Since the set is directly proportional, you'd use $k={\frac {20}{4}}=5$ . Your constant of proportionality is $5$ .
- What about the inverse set? Take the ratio ${\frac {1}{12}}$ and plug the numbers into the equation $k=yx$ to get $k={(1)}{(12)}=12$ . Your constant of proportionality is $12$ .
4
Check your work with the other ratios. If the ratios are proportional, the constant of proportionality will be the same for all of them. If any of them are different, then the ratios aren't proportional and there is no constant of proportionality.^{[8]
X
Research source}
- Try this on your own with the ratios in the set ${\frac {20}{4}}$ , ${\frac {40}{8}}$ , and ${\frac {60}{12}}$ . You'll see that you get $5$ for each ratio, which tells you this ratios are indeed directly proportional!
- This also applies to ratios that are inversely proportional. For example, in the set ${\frac {1}{12}}$ , ${\frac {2}{6}}$ , and ${\frac {3}{4}}$ , plugging each ratio into the equation $k=yx$ gets you a constant of $12$ for each ratio, so they are inversely proportional.
5
Determine other values in the series using the constant of proportionality. Now that you know the constant of proportionality, you can figure out what the value of $y$ $y$ would be for any value of $x$ $x$ .^{[9]
X
Research source}
- Use the equation $y=kx$ if the set of ratios is directly proportional. If $x$ is $7$ and $k$ is $5$ , $y$ would be $35$ ( $y=(7)(5)=35$ ).
- Use the equation $y={\frac {k}{x}}$ if the set of ratios is inversely proportional. If $x$ is $4$ and the constant of proportionality is $12$ , $y$ would be $3$ ( $y={\frac {12}{4}}=3$ ).

Section 4 of 6:

Practice Problems

1
Find the constant of proportionality for ${\frac {10.5}{1.5}}$ , ${\frac {14}{2}}$ , ${\frac {24.5}{3.5}}$ , and ${\frac {35}{5}}$ .^{[10]
X
Research source}
- Hint: All of the values increase, so use the equation for direct proportionality: $k={\frac {y}{x}}$ .
2
Find the constant of proportionality for ${\frac {105}{-2}}$ , ${\frac {-105}{2}}$ , ${\frac {-35}{6}}$ , ${\frac {-21}{10}}$ , and ${\frac {-15}{14}}$ .^{[11]
X
Research source}
- Hint: The $y$ values are decreasing, so use the equation for inverse proportionality: $k=yx$ .
3
The slowest mammal in the world, the sloth, moves at a rate of $6$ feet per minute. How far will Flash the sloth have gone in $5$ minutes? And how long will it take Flash to complete the 100-yard dash?^{[12]
X
Research source}
- Hint: 100 yards is 300 feet.
4
You're on a road trip. Each time you get gas, you record the number of miles you drove and the amount of gas your car used: $224$ miles on $8$ gallons, $280$ miles on $10$ gallons, and $112$ miles on $4$ gallons. What is your car's gas mileage?^{[13]
X
Research source}
- Hint: Gas mileage is the number of miles your car can drive on one gallon of gas, so you're looking for the constant of proportionality here.

Section 5 of 6:

Solutions to Practice Problems

1
The constant of proportionality is $7$ . If you remember your multiplication tables, you know that ${\frac {14}{2}}$ ${\frac {14}{2}}$ and ${\frac {35}{5}}$ ${\frac {35}{5}}$ simplify to $7$ $7$ . When you do the basic math for the other two ratios in the set, you find that both ${\frac {10.5}{1.5}}$ ${\frac {10.5}{1.5}}$ and ${\frac {24.5}{3.5}}$ ${\frac {24.5}{3.5}}$ also simplify to $7$ $7$ , so that's your answer.^{[14]
X
Research source}
- Since all the ratios in the set have the same constant and the values are all increasing, you also know that this series is directly proportional.
2
The constant of proportionality is $-210$ . Since the $y$ $y$ values are decreasing, you simply multiply the numbers together to get a value for the constant of proportionality, $k$ $k$ using the equation $k=yx$ $k=yx$ . Before you even start multiplying, you can already tell that each of the ratios is going to simplify to a negative number. All that's left is to multiply each ratio to see that they all simplify to $-210$ $-210$ :^{[15]
X
Research source}
- For ${\frac {105}{-2}}$ , $k=(105)(-2)=-210$ .
- For ${\frac {-105}{2}}$ , $k=(-105)(2)=-210$ .
- For ${\frac {-35}{6}}$ , $k=(-35)(6)=-210$ .
- For ${\frac {-21}{10}}$ , $k=(-21)(10)=-210$ .
- For ${\frac {-15}{14}}$ , $k=(-15)(14)=-210$ .
- Since all of the ratios have the same constant of proportionality, they are inversely proportional.
3
Flash will go $30$ feet in $5$ minutes and complete the 100-yard dash in $50$ minutes. Start this problem by finding the constant of proportionality. You know you're going to be working with directly proportionate ratios because the more minutes pass, the further Flash will go, so you use the equation $k={\frac {y}{x}}$ $k={\frac {y}{x}}$ . The distance Flash goes depends on how long he's moving, so distance is the $y$ $y$ variable and time is the $x$ $x$ variable. You've been told that Flash goes $6$ $6$ feet in $1$ $1$ minute, so that makes his constant of proportionality $6$ $6$ ( $k={\frac {6}{1}}=6$ $k={\frac {6}{1}}=6$ ).^{[16]
X
Research source}
- To find how far Flash will go in $5$ minutes, use the equation for direct proportionality, $y=kx$ . Here, $x$ is $5$ , so your answer is $30$ ( $y=(6)(5)=30$ ).
- To find out how long it will take Flash to complete the 100-yard (300 feet) dash, use the same equation, but solve for $x$ instead. Start with $300=6x$ , then divide each side by $6$ to get your answer, $50$ .
4
Your car gets $28$ miles to the gallon. The numbers for gallons of gas aren't in sequential order, but if you shuffle them around, you see that the values for both gas and miles driven are increasing—so this is a direct proportionality problem. The number of miles you drive depends on the gallons of gas you have in your car, so miles driven is the $y$ $y$ variable, and gallons of gas is the $x$ $x$ variable. Now, all you need to do is plug those values into the equation for direct proportionality:^{[17]
X
Research source}
- $k={\frac {224}{8}}=28$
- $k={\frac {280}{10}}=28$
- $k={\frac {112}{4}}=28$

Section 6 of 6:

How can you tell if ratios are proportionate?

1
Plot the points on a graph and draw a line through the points. If the line you drew crosses the origin of the graph, the points have a proportional relationship. But if the line doesn't go through the origin, the points are not proportional.^{[18]
X
Research source}
- When graphing ratios, the first number (or numerator of a fraction) is the $y$ coordinate and the second number (or denominator of a fraction) is the $x$ coordinate.^{[19]
  X
  Research source}
2
Find the constant of proportionality for each ratio. If any of the ratios in the set has a different constant of proportionality than the others, the ratios in the set are not proportional. But if all of the ratios have the same constant of proportionality, then they are proportional.^{[20]
X
Research source}
- Remember to use $k={\frac {y}{x}}$ if the values of both variables go up and $k=yx$ if the value of one variable goes up and the other goes down.