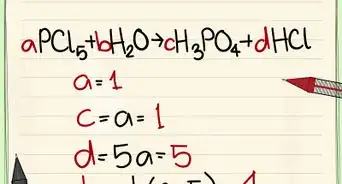X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time.
This article has been viewed 49,884 times.
Learn more...
Balancing chemical equations is typically done by first identifying uncommon elements in compounds and working your way towards hydrogen and oxygen. There is also a slower but more systematic approach using linear algebra.
Steps
-
1Identify the equation to balance.
-
2Identify the elements. The number of elements present in the equation determines how many rows will be in the vectors and matrices that we are going to construct. Below, the order we list corresponds to the order of the rows.
- – Hydrogen
- – Phosphorus
- – Oxygen
- – Nitrogen
- – Molybdenum
Advertisement -
3Set up the vector equation. The vector equation consists of column vectors corresponding to each compound in the equation. Each vector has a corresponding coefficient, labeled to for which we are solving for. Make sure you understand how to count the number of atoms in a molecule.
-
4Set the equation to 0 and obtain the augmented matrix. There are two major points to consider here. First, recognize that a vector equation like the one above has the same solution set as a linear system with its corresponding augmented matrix. This is a fundamental idea in linear algebra. Second, when the augments are all 0, row-reduction does not change the augments. Therefore, we need not write them at all – row-reducing the coefficient matrix is all that is necessary.
- Note that moving everything to the left side causes the elements on the right side to negate.
-
5Row-reduce to reduced row-echelon form. For such a matrix, it is recommended that you use a calculator, although row-reducing by hand is always an option, albeit slower.
- It is clear that there is a free variable here. Those with sharp minds would've seen this coming, for there are more variables than equations, and hence more columns than rows. This free variable means that can take on any value, and the resulting combination of to would be a valid solution (to our linear system, that is – the chemical equation results in further restrictions in this solution set).
-
6Reparameterize the free variable and solve for the variables. Let's set Since for positive values of none of the variables become negative, so we are on the right track.
-
7Substitute an appropriate value for . Remember that the coefficients in the chemical equation must be integers. Therefore, set the least common multiple. From our solution set, it is clear that while there are an infinite number of solutions, as we would expect, it is nonetheless a countably infinite set.
-
8Substitute the coefficients into the chemical equation. The equation is now balanced.
Advertisement
About This Article
Advertisement