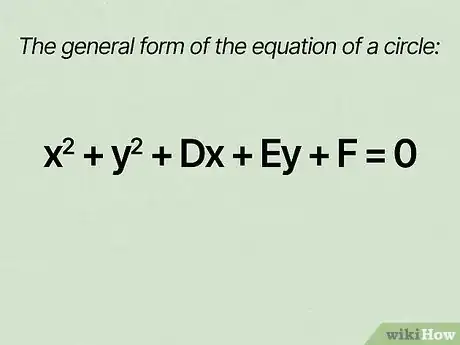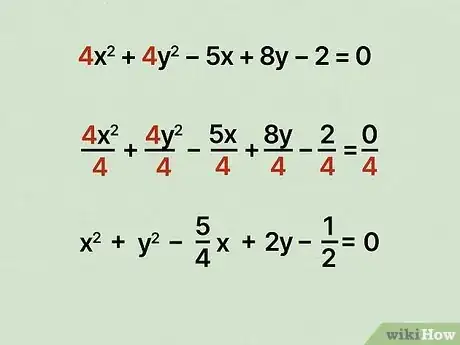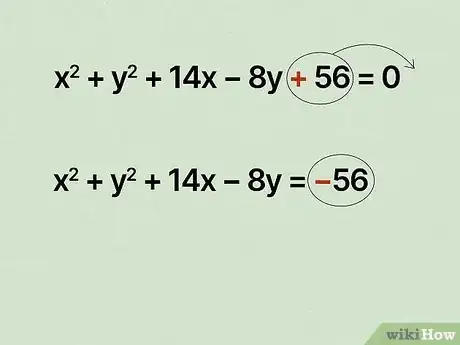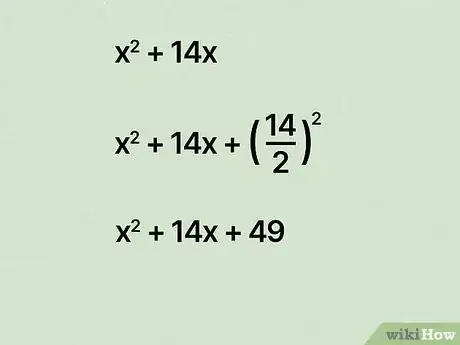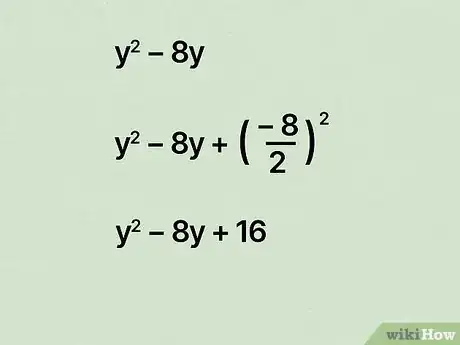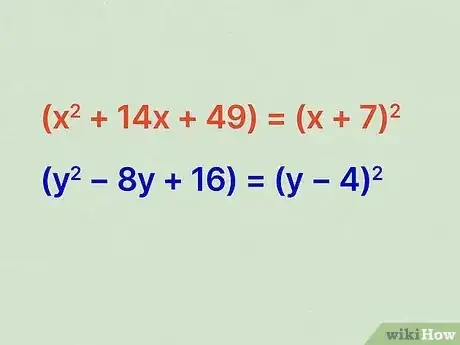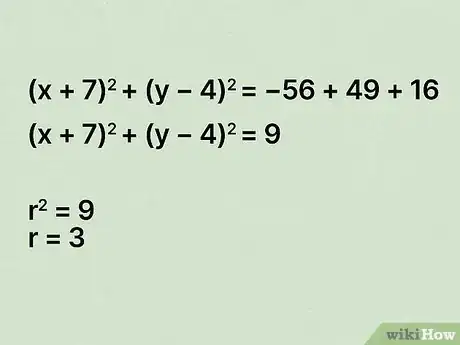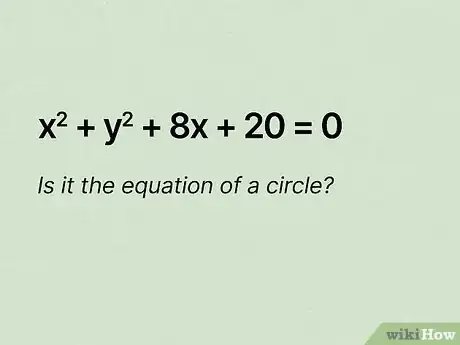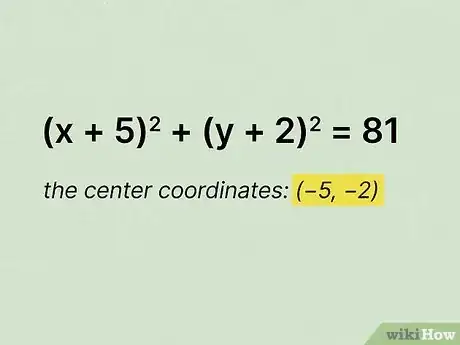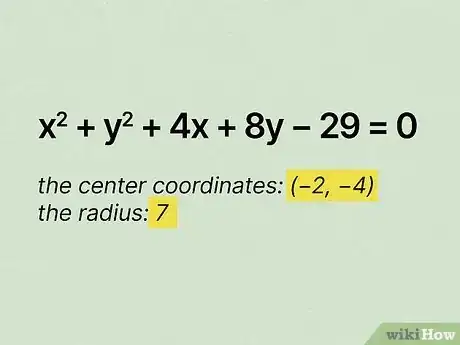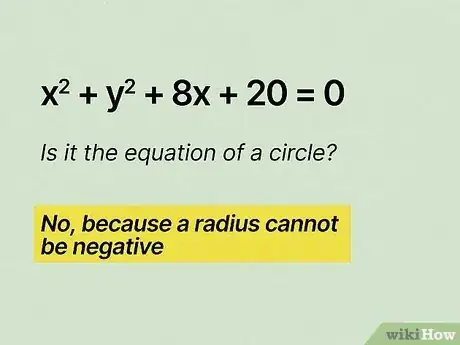Writing and Solving Equations of Circles

Co-authored by David Jia and Jennifer Mueller, JD

Last Updated: October 25, 2022 References

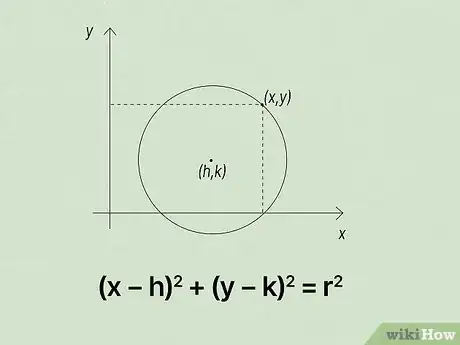
The equation of a circle gives you the center coordinates and radius, allowing you to represent all of the literally infinite points around the boundary of the circle. But how exactly do you write it? Read on to learn how to write the equation of a circle in standard form, as well as how to convert general form to standard form. Once you've got that down, you can try your hand at some sample problems and check your answers. Let's get started!

Things You Should Know

Write the standard form of the equation of a circle as $(x-h)^{2}+(y-k)^{2}=r^{2}$ to represent all points on a circle with the given center coordinates and radius.
Write the general form of the equation of a circle as $x^{2}+y^{2}+Dx+Ey+F=0$ . The general form isn't useful until you convert it to standard form.
Convert from general to the standard form by grouping like terms and completing the square to easily identify the center coordinates and radius of the represented circle.

Section 1 of 5:

Forms for Equations of Circles

1
The standard form of the equation of a circle is $(x-h)^{2}+(y-k)^{2}=r^{2}$ . In this equation, $x$ $x$ and $y$ $y$ represent any point on the circle while $h$ $h$ and $k$ $k$ represent the coordinates of the center of the circle. $r$ $r$ represents the radius of the circle. Let's break this down further so it's a little easier to understand:^{[1]
X
Research source}
- On a graph, $x$ tells you how many units from the center to go horizontally and $y$ tells you how many units from the center to go vertically to plot that point.
- Since $h$ is grouped with $x$ on the equation, it tells you how many units from the origin (that's point $0,0$ ) to go horizontally to plot the center of the circle.
- $k$ tells you how many vertical units from the origin to go to plot the center of the circle.
- When writing the equation of a circle, you always need to know the radius of the circle $(r)$ and the coordinates of the center of the circle $(h,k)$ .
2
The general form of the equation of a circle is $x^{2}+y^{2}+Dx+Ey+F=0$ . This equation technically has all the same information the standard form has, it's just expressed differently. Let's break it down:^{[2]
X
Research source}

$x$ and $y$ relate to the $x$ and $y$ axes of a graph.

The letters $D$ , $E$ , and $F$ in the form all represent numbers. For example, you might get the general form equation $x^{2}+y^{2}+2x+10y-1=0$ .

If you want to graph the circle or have a problem that asks you to identify the center coordinates or radius of the circle represented by a general equation, you have to convert the general equation to standard form.

Section 2 of 5:

Completing Basic Standard Form Problems

1
Use $x^{2}+y^{2}=r^{2}$ for a circle with its center point at the origin. When a circle's center is at the origin, the center coordinates are $(0,0)$ $(0,0)$ , which allows you to simplify the equation of the circle. This comes in handy if you have a problem that tells you to find the center. If one side or the other (or both) is simplified like this, you know the value for that coordinate is $0$ $0$ .^{[3]
X
Research source}
- For example, if you're asked to find the center coordinates of a circle with the equation $x^{2}+(y-2)^{2}=4$ , you know the $x$ coordinate is $0$ because of the origin equation. The number grouped with $y$ is $2$ , so the center coordinates are $(0,2)$ .
2
Plug in values for the radius and center coordinates to complete a standard equation. This is probably the simplest type of problem you'll have dealing with the equation of a circle. Just place the values where they go in the the standard form $(x-h)^{2}+(y-k)^{2}=r^{2}$ $(x-h)^{2}+(y-k)^{2}=r^{2}$ .^{[4]
X
Research source}
- For example, if you're given center coordinates of $(4,6)$ and a radius of $3$ , your equation of a circle would be $(x-4)^{2}+(y-6)^{2}=9$ . Remember the formula is $r^{2}$ , so you need to square $3$ for your final answer.
- If you're given the diameter, remember to divide it in half because the form calls for the radius.
3
Change the signs in parentheses when your center coordinates are negative. Sometimes, you'll be given negative center coordinates, such as $(-4,-6)$ $(-4,-6)$ . Since the sign in the parentheses of the standard form is $-$ $-$ , it becomes a positive, because $-(-x)=+x$ $-(-x)=+x$ .^{[5]
X
Research source}
- For example, if you have center coordinates $(-4,-6)$ and radius $3$ , your equation of the circle would be $(x+4)^{2}+(y+6)^{2}=9$ .
- Likewise, if you were asked to find the center coordinates for the circle with the equation $(x+1)^{2}+(y+3)^{2}=6$ , you would know that the signs had changed, so the center coordinates must be negative: $(-1,-3)$ .

Section 3 of 5:

Converting General Form to Standard Form

1
Divide to make the coefficients of $x^{2}$ and $y^{2}$ $1$ . If you have a number in front of $x^{2}$ $x^{2}$ and $y^{2}$ $y^{2}$ , divide everything in your equation by that number to get rid of it. Now you have a coefficient of $1$ $1$ . $x^{2}$ $x^{2}$ and $y^{2}$ $y^{2}$ must always have a coefficient of 1 so you can complete the square to convert the equation.^{[6]
X
Research source}
- For example, if you had $4x^{2}+4y^{2}-5x+8y-2=0$ , you would divide everything by $4$ , like so: ${\frac {(4x^{2})}{4}}+{\frac {(4y^{2})}{4}}-{\frac {5x}{4}}+{\frac {8y}{4}}-{\frac {2}{4}}={\frac {0}{4}}$ . You'd end up with $x^{2}+y^{2}-{\frac {5}{4}}x+2y-{\frac {1}{2}}=0$ .
- If the general form equation represents a circle, the two coefficients will always be the same number!
2
Move the constant to the other side of the equation. Since the number is moving to the other side of the equation, the sign in front of it changes. So if it was negative on the left side, it'll be positive on the right side (and vice versa).^{[7]
X
Research source}
- For example, $x^{2}+y^{2}+14x-8y+56=0$ would be $x^{2}+y^{2}+14x-8y=-56$ .
3
Group the $x$ terms and $y$ terms together. Now you'll do two mini-problems to complete the square for the $x$ $x$ terms and $y$ $y$ terms. Grouping them together makes it easier for you to do the math.^{[8]
X
Research source}
- For example, you would group $x^{2}+y^{2}+14x-8y=-56$ as $x^{2}+14x+y^{2}-8y=-56$ .
4
Divide the coefficient to complete the square for the $x$ group. Recall that to complete the square, you first divide the coefficient of the first term by 2. Since you've already gotten the coefficient to $1$ $1$ , this will always be ${\frac {1}{2}}$ ${\frac {1}{2}}$ . So divide the second coefficient by $2$ $2$ , then square it.^{[9]
X
Research source}
- For example, if you have $x^{2}+14x$ , divide $14$ by $2$ to get $7$ . Then square $7$ to get 49.
5
Divide the coefficient to complete the square for the $y$ group. Now you're going to do the same thing you did with the $x$ $x$ group with the $y$ $y$ group. Divide the second coefficient by $2$ $2$ , then square it.^{[10]
X
Research source}
- For example, if you have $y^{2}-8y$ , your number would be 16: $({\frac {-8}{2}})^{2}=(-4)^{2}=16$ .
6
Add the numbers to both sides of the equation. Keeping your groups together on the left side of the equation, add your third number to each parenthetical expression. Then, add each of those numbers to the right side of the equation to maintain equality.^{[11]
X
Research source}
- For example, from $x^{2}+y^{2}+14x-8y+56=0$ you now have $(x^{2}+14x+49)+(y^{2}-8y+16)=-56+49+16$ .
7
Solve the $x$ and $y$ groups. Now you have what you may recognize as a basic trinomial in each parenthesis. Use the quadratic formula to find the number you need for each parenthetical expression in the standard equation of a circle.^{[12]
X
Research source}
- For example, for $(x^{2}+14x+49)$ , you would get ${\frac {-14\pm {\sqrt {14^{2}-4*1*49}}}{2*1}}=-7$ . So your new parenthetical would be $(x+7)^{2}$ .
- Do the same thing with $(y^{2}-8y+16)$ to get $(y-4)^{2}$ .
8
Simplify the right side of the equation. Almost there! Add the numbers on the right side, then square them. The equation you're left with will be the standard form for the equation of a circle. From here, you can easily determine the center points and radius if you need to graph the circle.^{[13]
X
Research source}
- For example, if you've got $(x+7)^{2}+(y-4)^{2}=-56+49+16$ , you'd add the three numbers on the right side to get $(x+7)^{2}+(y-4)^{2}=9$ .
- The number on the right side represents the radius squared. So if you're asked for the radius, remember to take the square root of that number. In the example $(x+7)^{2}+(y-4)^{2}=9$ , it would be $3$ .

Section 4 of 5:

Practice Problems

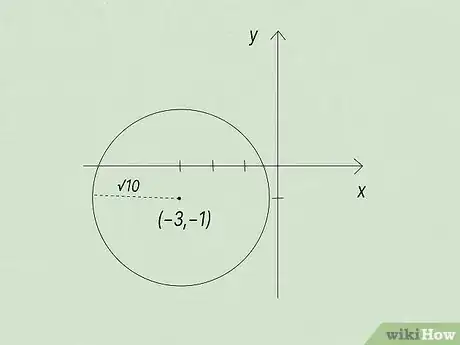
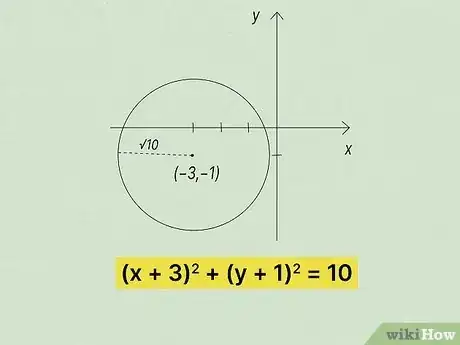
1
Write the equation of the circle with center $(-3,-1)$ and radius ${\sqrt {10}}$ .^{[14]
X
Research source}
- Hint: pay attention to the negative signs in front of the center coordinates.
2
Find the center coordinates of the circle with the equation $(x+5)^{2}+(y+2)^{2}=81$ .^{[15]
X
Research source}
- Hint: look at the signs in the parentheses and compare them to the standard form for the equation.
3
Find the center coordinates and radius for the circle $x^{2}+y^{2}+4x+8y-29=0$ .^{[16]
X
Research source}
Hint: complete the square twice to convert general form to standard form. Don't forget that anything you add on the left side you also have to add on the right side.
4
Is $x^{2}+y^{2}+8x+20=0$ the equation of a circle? Why or why not?^{[17]
X
Research source}
Hint: a circle can never have a negative radius.

Section 5 of 5:

Solutions for Practice Problems

1
The equation of the circle with center $(-3,-1)$ and radius ${\sqrt {10}}$ is $(x+3)^{2}+(y+1)^{2}=10$ . If you look at the radius first, you see that in the problem, it's expressed as a square root. A square root squared is just the number, so that part is easy. Then, plug in the values you have for the center in $(x,y)$ $(x,y)$ order to get your answer in standard form.^{[18]
X
Research source}
- Did you change the signs? Remember, two negatives make a positive, so the signs in the parentheses change to $+$ .
2
The center coordinates are $(-5,-2)$ . You're given the equation of the circle $(x+5)^{2}+(y+2)^{2}=81$ . Since the signs in the parentheses in the standard form are $-$ , the $+$ signs in this equation tell you that the center coordinates must be negative.^{[19]
X
Research source}
3
The center coordinates are $(-2,-4)$ and the radius is $7$ . You started with $x^{2}+y^{2}+4x+8y-29=0$ $x^{2}+y^{2}+4x+8y-29=0$ . Since this is the equation of a circle in general form, you need to convert it to standard form to solve the problem.After grouping like terms and moving the constant, $29$ $29$ , over to the right side, you get $x^{2}+4x+y^{2}+8y=29.$ $x^{2}+4x+y^{2}+8y=29.$ Now what?^{[20]
X
Research source}
- $x^{2}$ and $y^{2}$ already have a coefficient of $1$ , so you don't have to do anything there.
- Group like terms: $x^{2}+4x+y^{2}+8y-29=0$
- Move the constant to the right side of the equation: $x^{2}+4x+y^{2}+8y=29$
- Get the number you need to complete the square for the $x$ terms: $x=({\frac {4}{2}})^{2}=(2)^{2}=4$
- Get the number you need to complete the square for the $y$ terms: $y=({\frac {8}{2}})^{2}=(4)^{2}=16$
- Plug your numbers in to both sides of the equation: $(x^{2}+4x+4)+(y^{2}+8y+16)=29+4+16$
- Do the quadratic equation for the $x$ terms: ${\frac {-4\pm {\sqrt {4^{2}-4*1*4}}}{4*1}}=-2$
- Do the quadratic equation for the $y$ terms: ${\frac {-8\pm {\sqrt {8^{2}-4*1*16}}}{8*1}}=-4$
- Plug your parenthetical expressions into the standard form: $(x+2)^{2}+(y+4)^{2}=29+4+16$
- Add the numbers on the right side of the equation: $(x+2)^{2}+(y+4)^{2}=49$
- Take the square root of $49$ to find the radius.
4
This equation is not a circle because a radius cannot be negative. You started with $x^{2}+y^{2}+8x+20=0$ $x^{2}+y^{2}+8x+20=0$ . The first thing you do is move the constant over to the right side—and, of course, you have to change the sign, so now you have a $-20$ $-20$ on the right side of your equation. You don't have to complete the square for $y$ $y$ , but when you complete the square for $x$ $x$ , you get 16. This is as far as you have to go to see that this can't be the equation for a circle.^{[21]
X
Research source}
- Why? Because you're going to add $16$ to $-20$ . Since $16$ is smaller than $20$ , you know the result is going to be negative. But a radius can't be negative—so that's it. You've solved the problem. Great work!