This article was co-authored by Bess Ruff, MA. Bess Ruff is a Geography PhD student at Florida State University. She received her MA in Environmental Science and Management from the University of California, Santa Barbara in 2016. She has conducted survey work for marine spatial planning projects in the Caribbean and provided research support as a graduate fellow for the Sustainable Fisheries Group.
There are 16 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 15,226 times.
For many students, physics seems like a daunting and unapproachable subject. But, if you can explain that physics is meant to help us understand how the universe works, you can help your students feel more comfortable and excited to study it. To engage your class, illustrate abstract mathematical expressions with visual aids and practical examples whenever possible. For a basic introduction, review fundamental concepts, like the scientific method, then cover topics such as motion, force, work, and energy.
Steps
Introducing Fundamental Concepts
-
1Define physics as the study of matter in motion. Although physics is tough to define, explaining what your students will study in class can be a good starting point. Tell your students that physics aims to describe the most fundamental, or most basic, aspects of the universe. Physicists try to understand matter and the forces that govern its motion.[1]
- Mention that physics is one of the oldest academic fields and stems from humanity’s basic need to understand how the universe works.
- You could also bring up the discipline's impacts on human life. Explain that discoveries in physics led to feats from the smartphones in their pockets to nuclear technology.
- Connecting physics to basic human drives and discussing its impacts on life can help your students relate to the discipline and its aims.
-
2Review the scientific method. Your students have most likely taken other science courses, but it helps to explain how the scientific method works in physics. Start by listing the steps of the scientific method: observation, asking a question, forming a hypothesis, testing the hypothesis, analyzing the data, and forming a conclusion.[2]
- Remind your students that a hypothesis attempts to answer the question about what's been observed. For instance, a person might observe that things fall to the ground, and wonder if all objects fall at the same rate. They hypothesize that objects fall at different rates, and conduct experiments to test their claim.
- Suppose that, at first, their hypothesis in this example seems to be correct. They drop a feather and a rock, and see the objects fall at different rates. However, when they account for air resistance, they find that all objects on Earth fall at a rate of about 9.8 m/s2.
- Explain that physicists use mathematical expressions to express their hypotheses. They use math to hypothesize about an object's motion or a fundamental force.
Advertisement -
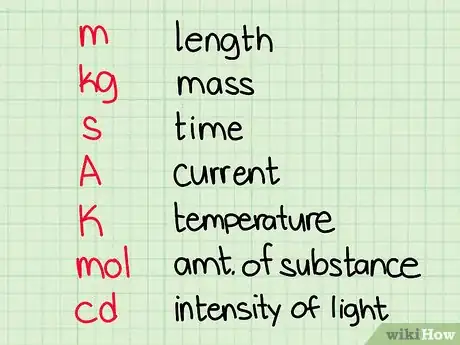
3Discuss the SI units of measurement. Tell your students that the sciences employ 7 standard units of measurement called the SI (système international, or international system) base units. These units are derived from natural constants, and help ensure measurements are accurate and standardized. The base units are:[3]
- The meter (m), which measures length.
- The kilogram (kg), or the unit of mass.
- The second (s), which measures duration.
- The ampere (A), which measures electrical current.
- The kelvin (K), the unit for temperature.
- The mole (mol), which measures the amount of substance, or the number of elementary particles in an object.
- The candela (cd), which measures the intensity of light.
-
4Show your students how to solve for variables. If your students have already taken algebra courses, remind them that they'll use formulas to find unknown quantities, or variables. For students that don't have a solid foundation in algebra, review how to work with known and unknown variables using equations.[4]
- Tell your students that they'll learn a variety of equations that include different variables, or letters that stand for measured quantities. They'll know some variables, and need to solve for others. The equations express mathematical relationships, which allows them to use the values they know to find an unknown variable.
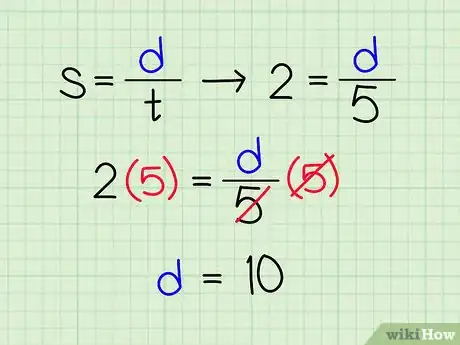
- The formula for speed is nice and simple, so it's a great way to introduce physics equations. Write “s = d/t” on the board, and say, “This is the formula to find speed. If I know d, or distance, and t, or time, I can divide d by t to find s.”
- Then continue, “I can rework this equation depending on my known and unknown variables. Suppose I know the variables s and t, but need to find d.” Write “s = d/t,” on the board then “2 = d/5” under it. Say, “Speed, distance, and time have a relationship. If I multiply 2, or time, by 5, or speed, I can find distance, or 10. If I travel at 2 meters per second for 5 seconds, I've traveled 10 meters.”
-
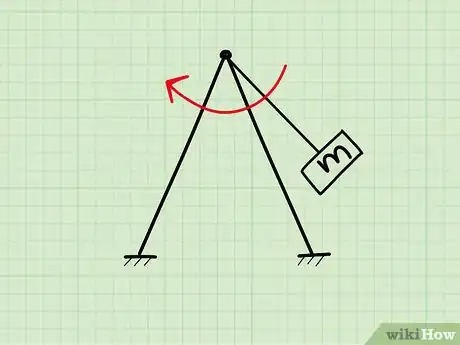
5Contextualize your examples. Students often find that they understand physics concepts better when they know how those concepts relate to the real world. For example, you could use roller coasters to explain potential and kinetic energy, or swings to demonstrate rotational dynamics.[5]
- Providing clear examples as you introduce terms not only helps your students understand what you're saying in the moment, it will help them relate more complex examples back to these concepts as they get further into your course.
Covering Basic Kinematics
-
1Start by introducing scalar and vector quantities. Tell your students that describing one-dimensional motion, or motion in 1 direction, is the most basic task in physics. Phrases like “going fast” and “slowing down” describe motion, but they're not very precise. Explain that, in physics, mathematical quantities called scalars and vectors are used to precisely describe an object's motion.[6]
- Define scalars as measurements that describe a magnitude alone, such as an object's speed or a distance. Offer examples of scalar quantities, such as a distance of 20 m, a speed of 10 m/s, and a mass of 100 g. Clarify that these numbers are scalars because they don't give information about direction.
- Explain that, in contrast, vectors describe both magnitude and direction, such as a velocity of 40 m/s north, an acceleration of 9.8 m/s2 downward, or a displacement of 25 m west.
- Try rolling a toy car forward, and say, “This car is moving 5 m/s west. Is this a vector or a scalar?” Then draw 2 rectangles on the board, connect them with an arrow labeled “10 m,” and say, “This brick has moved 10 m. We don't know the direction in which it has moved. Is this a vector or scalar?”
-
2Practice simple formulas by discussing speed and distance. Remind your class that speed and distance are scalar quantities, since they don't give information about direction. Explain that speed is the distance an object has traveled in a given amount of time. Show your students how the formula s = d/t expresses this relationship.[7]
- For a helpful visual example, take a meter-sized step as you count out 1 second. Say, “I traveled 1 meter in 1 second. My speed was 1 meter per second.”
- Then move a toy car and say, “Speed equals distance over, or divided by, time. Suppose this car has traveled 2 meters in 1 second. Let's fill in the formula s = d/t, so s = 2 m/1 s. The car's speed is 2 m/s. If it traveled 120 m in 3 seconds, s = 120 m/3 s, or 40 m/s.”
- Remind students that they can flip the formula around to find other missing variables. If they know the car's constant speed is 2 m/s, and it's been driving for 130 seconds, they can use the formula d = st to find the distance it traveled: d = (2)(130) = 260 m.
-
3Teach your students how to determine velocity. Tell your students that velocity is a vector, since it describes an object’s speed and its direction of motion. To help your students see how velocity works, move your toy car backward and forward to represent motion in each direction. On the board, write the formula vf = vi + at, where vf is final velocity, vi is initial velocity, a is acceleration, and t is time.[8]
- If a car’s initial velocity is 4 m/s west, and it accelerates at 3 m/s/s in the same direction for 5 s, its final velocity is (4) + (3)(5), or 19 m/s w.
- Emphasize that speed is distance traveled over time, but velocity is the rate at which an object changes its position. For example, if you walked forward 2 meters at a speed of 1 m/s, then back to the same spot at the same speed, your position didn't change. Since your position didn't change in this motion, your velocity is 0 m/s.
-
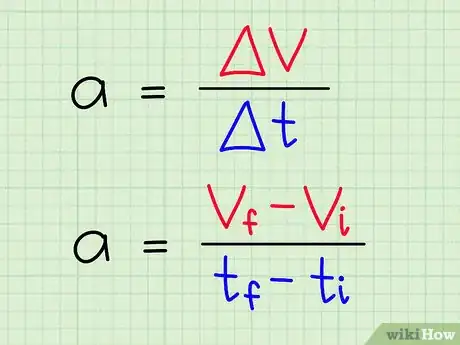
4Define acceleration as the rate of change in velocity. Explain that acceleration is the rate of change in velocity over a given period of time. It's a vector, since it gives a motion's direction. Write the equation a = Δv / Δt, on the board, and note that Δv (or vf - vi) is the change in velocity, and Δt (or tf - ti) is the amount of time.[9]
- For instance, if a car accelerates from 5 m/s to 8 m/s in 3 s, its average acceleration equals (8-5) / (3), or 1 m/s2.
- Mention that, on Earth, the acceleration of gravity is 9.8 m/s2. Explain that m/s2 means meters per second per second. This means a falling object accelerates (or changes its initial velocity) 9.8 m/s each second: 9.8 m/s at 1 second, 19.6 m/s at 2 seconds, 29.4 m/s at 3 seconds, and so on.
-
5Explain how to calculate displacement. Tell your students that displacement is the distance and direction of an object’s motion along a straight line. Show them the formula d = vit + ½at2, and say that vi is initial velocity, a is acceleration, and t is time.[10]
- To help your students see how displacement works, move your toy car and say, “This car's velocity is 5 m/s forward, and it accelerates at 2 m/s/s (meters per second per second, or m/s2) over a duration of 3 s.”
- Write the equation on the board: d = (5)(3) + ½(2)(3)2, or 15 + 9. Displacement equals 24 m forward.
-
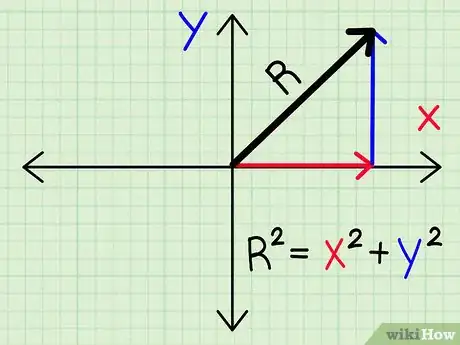
6Add two-dimensional motion to your lesson. Draw intersecting vertical and horizontal lines to make a large “+” shape. Tell your students that this is an xy graph. Explain that the vertical line, or y, is upward and downward motion, and the x axis is backward and forward motion.[11]
- Say, “Two-dimensional motion, or motion in 2 directions, involves 2 independent parts, which are called 'components.' Suppose I pull my dog's leash upward and backward (draw a diagonal line on the graph to represent the leash). This vector is made of 2 parts, or the upward component and a backward component. These parts are separate and independent from each other.”
- Now draw a cannon on the edge of a cliff. Draw a cannonball launched horizontally at 20 m/s, and add dots representing the ball as it moves forward and downward in a curved line. Tell your students that the vertical and horizontal components are independent motions.
- Say, “On Earth, gravity causes objects to fall at a rate of about 9.8 m/s. This means the cannonball's vertical velocity, or y increases by 9.8 m/s downward each second. At 1 second, vy = 9.8 m/s downward, at 2 seconds vy = 19.6 m/s down, and at 3 seconds it's moving 29.4 m/s downward. If there are no horizontal forces acting on the cannonball, its horizontal velocity, or vx remains constant at 20 m/s.”
-
7Show your students how to calculate a vector's components. Draw a diagonal line pointing up and to the right on the graph at a 60° angle. Label it “v = 50 m/s,” and tell your students that this represents the upward and forward motion of a cannonball. Now draw a rectangle around the diagonal line so the rectangle's lower left vertex is at one end of the line, and its top right vertex is at the other.[12]
- Write “60°” at the angle between the diagonal line, or the vector, and the rectangle's lower horizontal line. Explain that, “This angle can help us find the cannonball's horizontal velocity (point to the bottom of the rectangle) and vertical velocity (point to the right side of the rectangle).”
- Show your students that cosine and sine are ratios between a right triangle's angles and sides. Point to the 60° angle and say, “The ratios between this angle, the diagonal line, or the hypotenuse, and the horizontal and vertical lines can help us find unknown variables.
- We know the velocity, or the diagonal line is 50 m/s at 60° above the horizontal. To find the horizontal line, or vx, we'll multiply the diagonal line by the cosine of the angle. This means vx = (50 m/s)(cos60°). The cosine of 60° is 0.5, so vx = 25 m/s forward.”
- Next, explain how to find the vertical component. Point to the vertical line and say, “To find this value, or the upward component of the object's motion, we'll multiply the sine of the 60° angle by the object's velocity: vy = (50 m/s)(sin60°), or about 43 m/s upward.”
Explaining Force, Work, and Energy
-
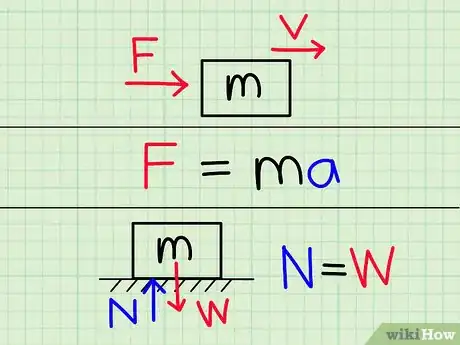
1Discuss forces and Newton’s laws. Tell your students that Newton’s laws of motion are the foundation of classical physics. They explain the relationships between an object and the forces that act on it. Mention that, in prior examples, they calculated the car’s linear motion, but now they have to account for the forces that govern how it moves.[13]
- The first law of motion, or the law of inertia, states that any object in motion will stay in motion at the same speed and same direction unless another force acts on it. Say, “Imagine a hockey puck rolling over ice. The force of friction slows the puck, so it doesn't travel forever. If the ice were perfectly frictionless, the puck would stay in motion.”
- Newton’s second law states that the force acting on an object determines its change in momentum. This law gives us the equation F = m / a, which we can use to find the magnitude of a force. F is force (measured in newtons), m is the object’s mass, and a is its acceleration. Roll your toy car forward, then give it additional pushes forward and backward. Tell the class that second law explains how the backward and forward forces change the car's motion.
- The third law states that every action has an equal and opposite reaction. Say, “If a road exerts frictional force on a car’s tires, the car’s tires also exert friction on the road. When you sit on a chair, you exert a downward force on it, and it exerts an upward force on you.”
-
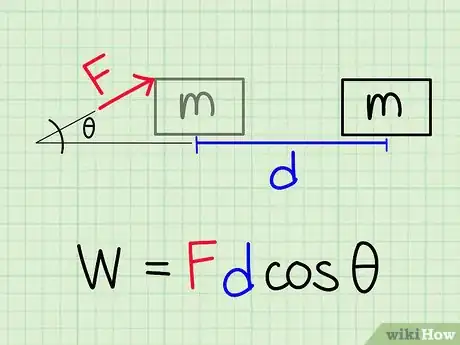
2Explain that work is the action of a force. Tell your students that work is what a force does, or how much it moves an object. Work transfers energy from one object to another. Energy is needed in order for one object to move, heat, or affect another.[14]
- Write the formula W = Fd cosθ on the board, where W is work, F is force, d is displacement, and cosθ is the cosine of the angle between the force direction and the object’s direction of motion. Mention that the unit of measurement for work is joules, which is 1 newton of force exerted over 1 meter, or 1 N multiplied by 1 m.
- Note that if the direction of the force and the direction of the object’s motion are the same, the angle between them is 0°, and the cosine of 0 is 1.
- To offer an example, say, “Suppose a person is pushing a lawn mower at a downward angle of 60° with a force of 900 N, and they’ve pushed the lawn mower 30 m. To calculate work, enter the variables into the equation (write them on the board): W = (900)(30)(cos60°). The cosine of 60° is 0.5, so W = (27,000)(0.5), or 13,500 J.”
-
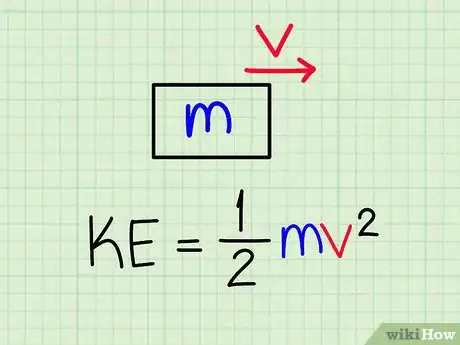
3Show your students how to calculate kinetic energy. Explain that energy is the ability to do work, and there are 2 forms. Tell them potential energy is stored energy, and kinetic energy is the energy of a moving body. For example, if you’re at the top of a hill, you have more potential energy than at the bottom. If you roll down the hill, you convert your potential energy into motion.[15]
- As you write the formula on the board, say, “To calculate kinetic energy, which is measured in joules, use the formula KE = ½mv2. The m stands for mass and v is velocity. Suppose a bowling ball that weighs 5 kg is rolling at 3 m/s. Plug the variables into the equation to find its kinetic energy: KE = ½(5)(3)2, or 16 J.”
-
4Provide examples of potential energy. Show your students a spring or an elastic band, stretch it out, and explain that it's storing elastic potential energy. Tell them a flying object, on the other hand, stores gravitational potential energy. If it falls, it converts this potential energy into kinetic energy.[16]
- To calculate elastic potential energy, or energy stored in a spring, write the formula U = ½kx2 on the board. Explain that k refers to the spring’s stiffness, or its spring constant, and x is how far it’s been stretched. For example, if a spring with a spring constant of 10 N/m has been stretched 1 m, its potential energy is ½(10)(1)2, or 25 J.
- To find the gravitational potential energy (on Earth), show them the formula U = mgh, where m is the object’s mass, g is the Earth’s gravitational constant (9.8 m/s2), and h is the object’s height. Tell them, “Suppose a drone weighs 2 kg and is flying at a height of 100 m. Its gravitational potential energy equals (2)(9.8)(100), or 1,960 J.”
Doing Hands-on Activities
-
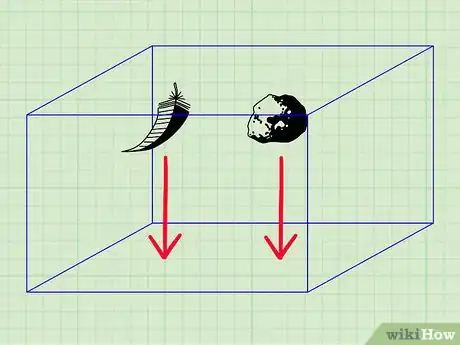
1Use a vacuum container to show that gravity is constant. Start by dropping a small rock and a feather at the same height. Ask your class which one will fall to the ground faster. After the first test, place the feather and rock in a vacuum-sealed container, flip it over, and show the students how the objects now fall at the same rate.[17]
- Tell your students, “Outside of the vacuum container, the feather doesn’t fall more slowly because it weighs less than the rock. The feather has more surface area and collides with particles of air. This is called air resistance, and if you remove the air, the objects fall at the same rate.”
- Since it’s so counterintuitive, this is a good introductory experiment, especially for younger students. It can help them see how many variables are involved in motion and force.
-
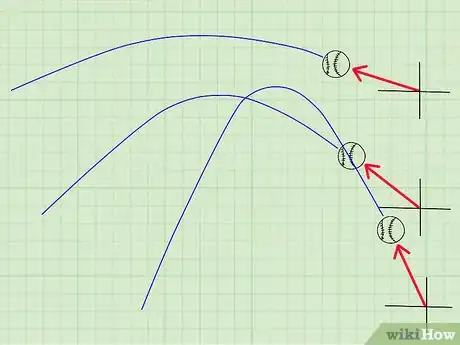
2Throw balls at different angles to explore vectors and parabolas. First, you or a student will throw a ball at a 15° angle, or as parallel to the ground as possible. Then, throw the ball at a 45° angle and, finally, throw it high, but not straight up, or at a 75° angle. Have a student mark where balls thrown at shallow, medium, and steep angles land.[18]
- Before throwing the balls and marking distances, ask students to make predictions about how balls thrown at each angle will travel. They can answer verbally or write their answers on a handout.
- Have your students closely observe the balls as they’re thrown. Showing slow-motion videos of balls being thrown could also be helpful. Point out the curved shape of the balls’ trajectories, and label this term “parabola.”
- Explain, “Balls thrown at medium angles usually travel the farthest. Gravity pulls balls thrown at shallow angles down sooner, so they don’t have time to travel far. Balls thrown higher spend more energy resisting gravity than they do traveling forward.”
- Throw the balls as hard as you can so the throwing force remains relatively consistent. For a bonus lesson, use various types of balls, such baseballs and wiffle balls, to explore how shape, weight, and drag affect the results.
-
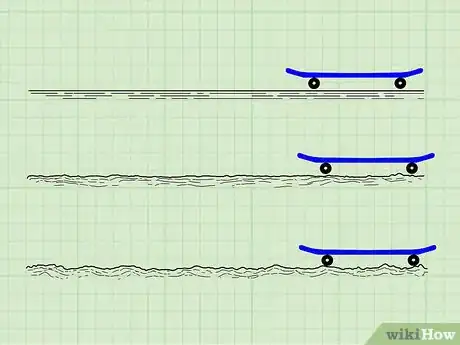
3Demonstrate motion, force, and friction with skates or a skateboard. To start, you or a volunteer will stand on a skateboard or wear roller skates. Have students take turns gently pushing and pulling the skater over various surfaces and with different degrees of force.[19]
- Measure how far a push sends the skater over rough, bumpy pavement. Note how far a push of the same force sends the skater over a smooth surface. Give the skater a gentle push or pull as they're already moving forward.
- Tell your class, “Friction slows down the skater’s motion, even if the same force was applied. When they’re moving forward, a push forward increases their forward motion.”
- Make sure the skater wears a helmet and pads, and instruct your students to pull or push gently and slowly. A spotter can help the skater stay on their feet. If you’re worried about accidental injuries, use a skateboard without a rider or a cart.
- For a bonus lesson, have the skater carry textbooks or place objects in the cart. Point out that, as Newton’s second law states, the same force applied to objects with less mass makes them travel farther
-
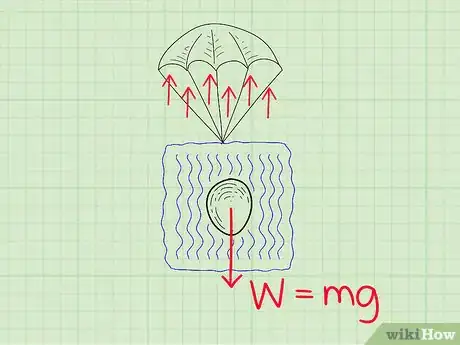
4Do the classic egg drop experiment. Provide plastic bags, tape, cardboard tubes, bubble wrap, paper, straws, and other cushioning materials. Have groups of students construct protective casings for an egg, then drop the eggs from a 1-story window or stair landing.[20]
- Consider making a protective case of your own with ample lightweight cushioning around the egg and a well-constructed parachute, just in case none of the groups create a successful design.
- Point how how a parachute lowers the rate of descent, and explain that the egg converts potential energy to kinetic energy as it falls.
- Write out the formula for kinetic energy (KE = ½mv2) and say, “A smaller mass and lower velocity means lower kinetic energy. The parachute lowers the egg’s velocity, and lightweight cushioning protects the egg, but keeps the overall mass low.”
References
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion/introduction-to-physics-tutorial/a/what-is-physics
- ↑ http://teacher.pas.rochester.edu/phy_labs/appendixe/appendixe.html
- ↑ https://www.bipm.org/en/measurement-units/
- ↑ https://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity
- ↑ http://www.bsharp.org/physics
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion
- ↑ https://www.physicsclassroom.com/Class/1DKin/U1L1b.cfm
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion
- ↑ https://www.physicsclassroom.com/class/vectors/Lesson-1/Independence-of-Perpendicular-Components-of-Motion
- ↑ https://www.physicsclassroom.com/Class/vectors/u3l2d.cfm
- ↑ https://www.khanacademy.org/science/physics/forces-newtons-laws
- ↑ https://www.khanacademy.org/science/physics/work-and-energy
- ↑ https://www.khanacademy.org/science/physics/work-and-energy
- ↑ https://www.khanacademy.org/science/physics/work-and-energy
- ↑ https://www.physicsclassroom.com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance
- ↑ https://www.scientificamerican.com/article/the-physics-of-baseball-how-far-can-you-throw/
- ↑ https://serc.carleton.edu/sp/mnstep/activities/19858.html
- ↑ https://stem.neu.edu/programs/ayp/fieldtrips/activities/eggdrop/
- ↑ https://www.wired.com/2014/05/5-reasons-you-should-consider-a-different-physics-textbook/
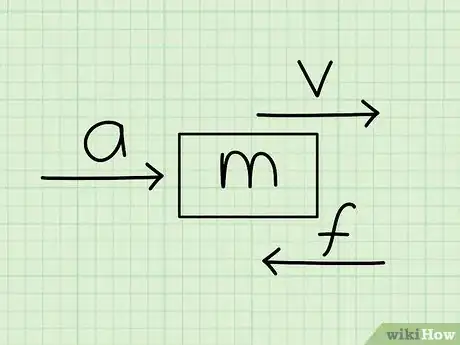


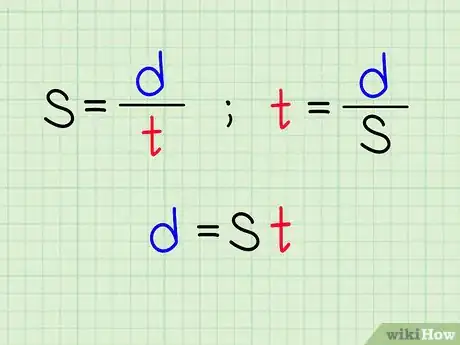
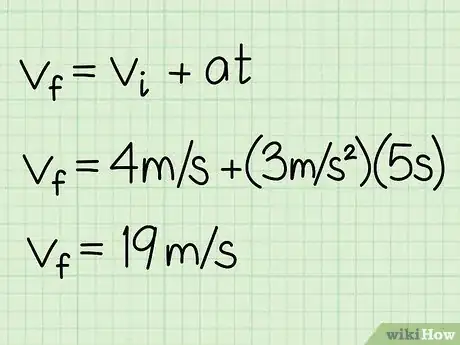

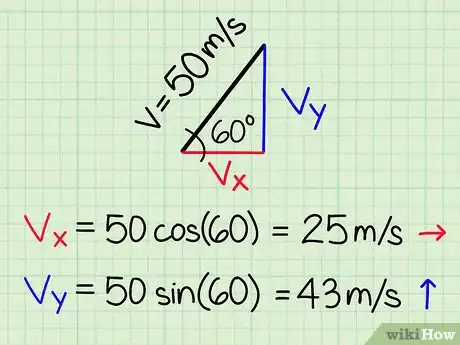
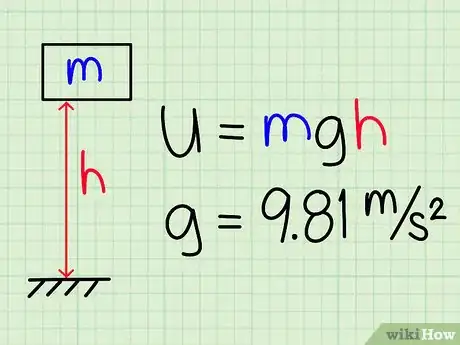





-Step-15.webp)