How to Solve Sudoku when Stuck

Co-authored by Hunter Rising

Last Updated: August 30, 2022 References

So you’ve filled in all of the numbers you can on a sudoku puzzle, but now you’re stumped on what to fill in next. Even though you can always work out the solution for sudoku, you may have to try a few different strategies to figure out exactly where a number is supposed to go. If you want to know the best basic and advanced techniques to use when you’re stuck, keep reading so you can learn how to finish the puzzle!

1

Notation

Writing down possible numbers for each cell lets you see your options. Since numbers can only appear once in each row, column, and 3 x 3 box in the puzzle, the candidates you can put in the empty squares are limited. Go through each cell and scan the row, column, and box that it’s in to figure out what numbers could still fit there. Write all of the potential candidates in the cell lightly with a pencil.^{[1]
X
Research source}
- If seeing all of the possible numbers in the cells looks overwhelming, only notate the squares that have 2 or 3 potential numbers instead.

2

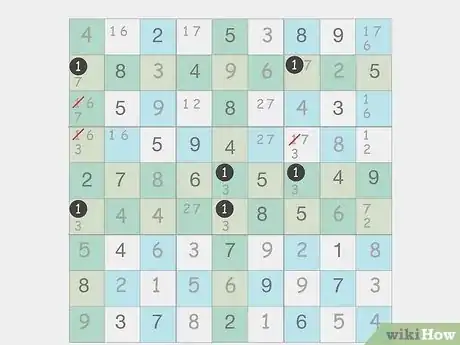
Sole candidate

If only one number fits in a cell, then it has to go there. After you fill in your notation, you might find some obvious cells to fill in that you missed earlier. Scan through each of the cells on the puzzle and see if there are any with just one possible solution. Since you know that no other numbers can fit there, that number is the only solution for that cell.^{[2]
X
Research source}
- Once you fill in the number, check the row, column, and box that the cell was in and erase any other instances of that number.
- Be on the lookout for “hidden singles” as well. You can fill in a number if it isn’t written down anywhere else in the same row, column, or box, even if there are other candidates in that cell.

3

Naked and hidden pairs

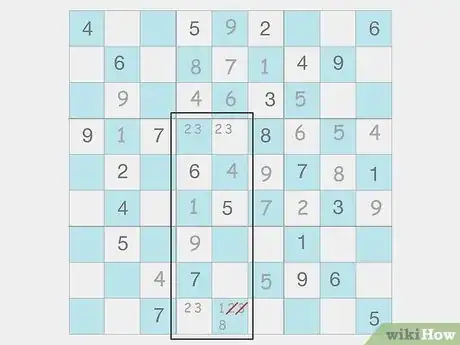
Cells with 2 numbers in the same row, column, or box limit other cells. Check for 2 cells in the same row, column, or box that can only contain the same 2 possible numbers, which is known as a “naked pair.” Even though you don’t know exactly which number goes into each square, you can erase your notation for the other cells in the row, column, or box since they can never contain those values.^{[3]
X
Research source}
- “Hidden pairs” are similar but a little trickier to find. The 2 cells are the only places where the numbers can be placed, but the cells may have notation for other potential candidates.

4

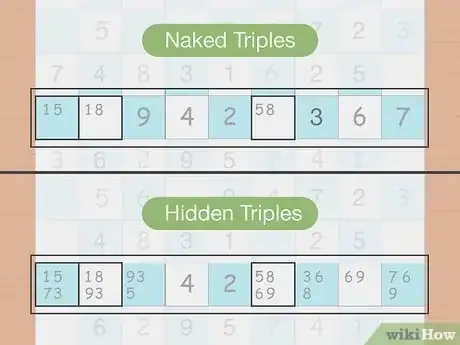
Naked and hidden triples

Triples have only 3 possible numbers that could fit into the 3 cells. All 3 cells have to be in the same row, column, or box. “Naked” triples only have the 3 potential numbers while “hidden” triples have extra digits in the cells that make them harder to spot. All 3 of the potential candidates don’t have to appear in each of the cells, which can make them a little trickier to find.^{[4]
X
Research source}
- Example: If the cells contain 1 & 5, 1 & 8, and 5 & 8, the values 1, 5, and 8 have to go into those cells and can’t be written in other cells in the same row, column, or box.

5

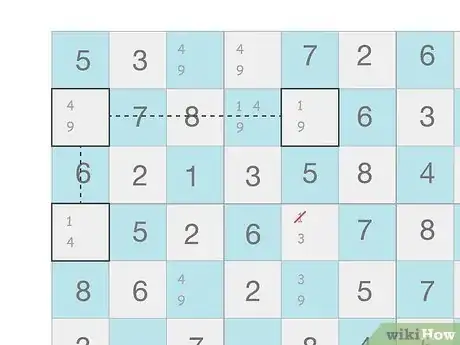
Pointing pairs and triples

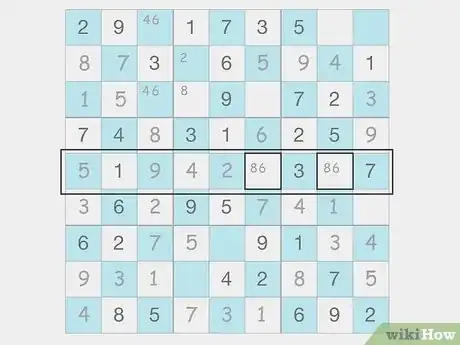
Eliminate numbers from a row or column if they’re constrained to one box. Pointing pairs and triples are when there are only 2 or 3 cells with the same potential numbers in a 3 x 3 box. The cells must also be in the same row or column. Since you know that the number has to go in one of those 2 cells, you can erase any other time you notated the number in the same row or column.^{[5]
X
Research source}
- Example: If A1 and C1 are the only cells in a box with 4 as a potential candidate, you can erase all other 4s from the first column.
- Example: If D4, D5, and D6 are the only spots in the middle box that can contain 8, no other cells in the D row can have 8.
- You won’t know which cell the number goes into quite yet, but pointing pairs and triples should help narrow down your options for other cells.

6

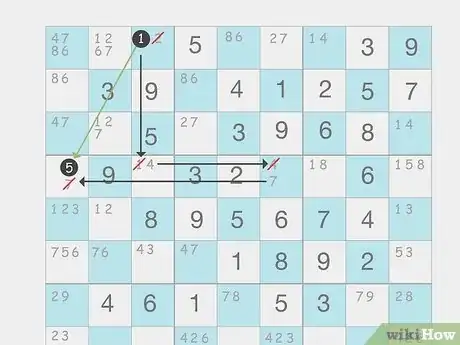
Forcing chain

Test a number in a cell with 2 digits to see how it affects the other cells. To use a forcing chain, look for multiple cells that have 2 potential numbers. You should be able to draw lines through the rows and columns to connect all the cells in the chain. Test each number in one of the cells and check how they fill in the rest of the chain. If there’s one cell that uses the same number no matter which digit you filled in originally, then you can assume that it’s the only solution.^{[6]
X
Research source}
- Mark the square you started in so you can retrace your steps.

7

X-wing

The X-wing technique reveals numbers for cells in 2 columns and rows. To use an X-wing, check for a row that has a potential candidate that can only fit into 2 cells. Check for another row in the puzzle that has the same candidate in 2 cells that are in the same columns as the first row candidates. The potential number can only fit once in each of the columns, so you can erase it from any other cells in those columns.^{[7]
X
Research source}
- Example: If a 2 could only be in the 1st and 7th columns in rows E and G, then you can erase 2 as a potential candidate from all other cells in those rows.

8

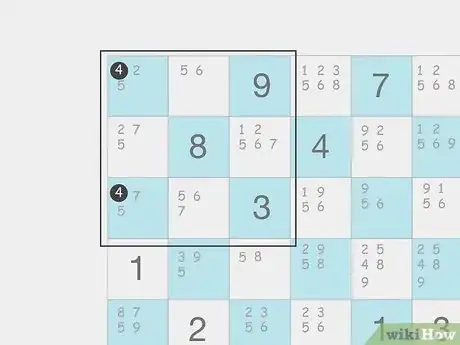
Y-wing

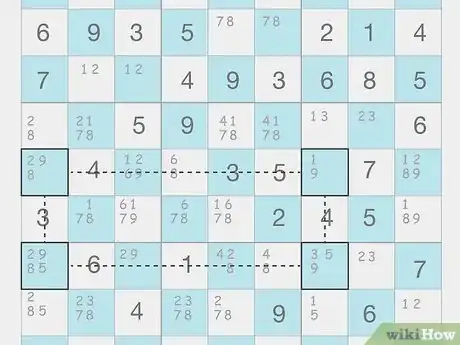
You can eliminate numbers from intersections between rows and columns. Start by finding a cell with only 2 possible numbers to use as a “pivot.” Check the same row, column, and box for “pincers”, which are other cells with 2 potential candidates that share at least 1 number with the pivot. The second number in each of the pincers should be the same. Check the cell where the pincers would intersect on the puzzle to see if it shares a number with them. If it does, then you can eliminate it from the puzzle.^{[8]
X
Research source}
- Example: A2 is the pivot with 3 & 8. The pincers are I2 with 4 & 3 and A6 with 4 & 8. The intersection between I2 and A6 is I6 with 4 & 5. Since 4 is in both of the pincer cells, you can eliminate it as an option from I6.

9

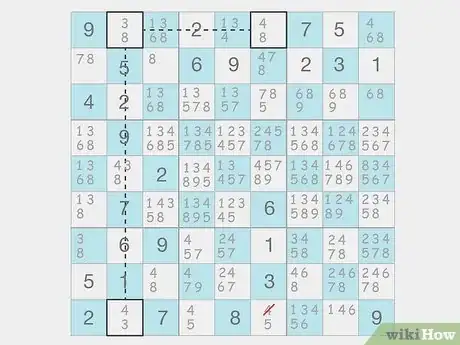
XY-wing

Rule out numbers when 3 cells with 2 values each form an angle. The values should only have 3 different potential numbers between them. If one cell has candidates X and Y and the other 2 cells could be X and Z or Y and Z, then no other cells in the same row, column, or box can contain the Z value.^{[9]
X
Research source}
- Forming an angle means that 2 of the cells are in the same row or column, but the third cell can be positioned anywhere that shares a row, column, or box with one of the others.
- Example: B1 could be 4 or 9, B5 could be 1 or 9, and D1 could be 1 or 4. The cell D5 couldn’t be 1 since it would make filling in B1 impossible. That means you can eliminate 1 as a candidate from D5.

10

Swordfish

Test the possibilities in a chain of numbers found in 3 rows or columns. Check your puzzle for 3 separate rows or columns where a potential digit can only fit into 2 or 3 cells in each. You should be able to connect the cells if you drew lines through the columns and rows. After you connect all of the cells you can erase the potential candidate from any other cells in those rows or columns.^{[10]
X
Research source}
- Example: The only cells in rows B, E, and F that can contain 1 are B1, B7, E5, E7, F1, and F5. Since you can draw a closed loop connecting these cells, you can erase 1 from any other cells in the same columns as these cells.

11

Unique rectangle

Unique rectangles work if 4 cells have the same pair of numbers. Every sudoku puzzle has a unique solution, but you might be faced with multiple possibilities if there are 2 sets of 2 cells in the same row, column, or box that have the pair of potential numbers. Check if any of the 4 cells have additional candidates in them. If so, then you can erase the original pair of digits since it would make the puzzle impossible to solve.^{[11]
X
Research source}
- Example: 2 & 3 are the only potential candidates in D4, D5, and I4. I5 has 1, 2, 3, & 8 as potential candidates. With a unique rectangle, you can eliminate 2 & 3 as options from I5.