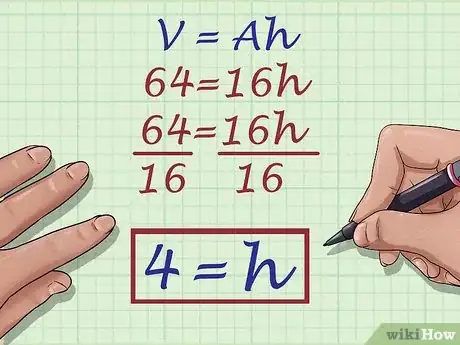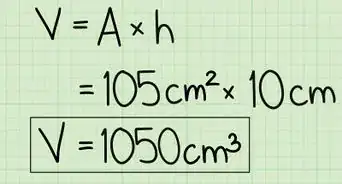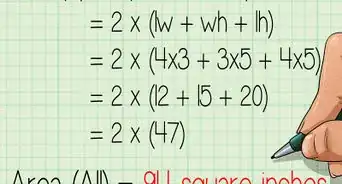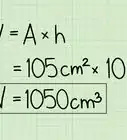How to Find The Height Of a Prism

Co-authored by wikiHow Staff

Last Updated: December 1, 2022 References

A prism is a three-dimensional solid with two parallel bases, or faces, that are congruent.^{[1]
X
Research source} The shape of the base determines what type of prism you have, such as a rectangular or triangular prism. Because it is a 3D shape, finding the volume (space inside) of a prism is a common task; however, sometimes you will need to find the height of a prism. Finding the height is possible if you have enough information already given: either the volume, or the surface area and perimeter of the base. The formulas described in these methods can work for prisms with bases of any shape, provided you know the formula for finding the area of that shape.

Method 1

Method 1 of 4:

Finding the Height of a Rectangular Prism With a Known Volume

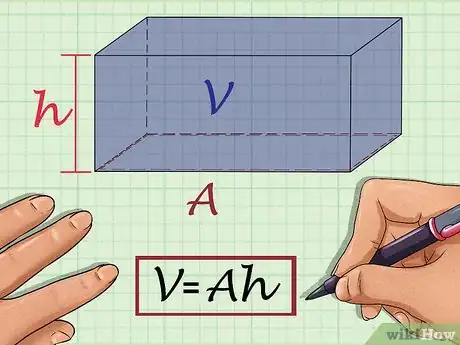
1
Set up the formula for the volume of a prism. The volume for any prism can be found by using the formula $V=Ah$ $V=Ah$ , where $V$ $V$ equals the volume of the prism, $A$ $A$ equals the area of one base, and $h$ $h$ equals the height of the prism.^{[2]
X
Research source}
- The base of a prism is one of its congruent sides. Since all opposite sides of a rectangular prism are congruent, any side can be used as the base, as long as you are consistent in your calculations.
2
Plug the volume into the formula. If you do not know the volume, you cannot use this method.
- For example, if you know the volume of the prism is 64 cubic meters ( $m^{3}$ ), then your formula will look like this:
  $64=Ah$
Advertisement
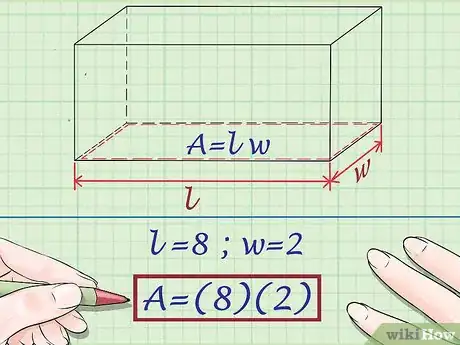
3
Find the area of the base. To find the area, you need to know the length and width of the base (or of one side, if the base is a square). Use the formula $A=lw$ $A=lw$ . To find the area of a rectangle.^{[3]
X
Research source}
- For example, if the base is a rectangle with a length of 8 meters and a width of 2 meters, to find the area you would calculate:
  $A=(8)(2)$
  $A=16m^{2}$
4
Plug the area of the base into the volume of a prism formula. Make sure you are substituting for the variable $A$ $A$ .
- For example, if you found the area of the base to be 16 square meters, then your formula will look like this:
  $64=16h$
5
Solve the equation for $h$ . This will give you the height of your prism.
- For example, if your equation is $64=16h$ , you would need to divide each side by 16 to find $h$ .Thus:
  ${\frac {64}{16}}={\frac {16h}{16}}$
  $4=h$
  So, the height of your rectangular prism would be 4 meters.

Method 2

Method 2 of 4:

Finding the Height of a Triangular Prism With a Known Volume

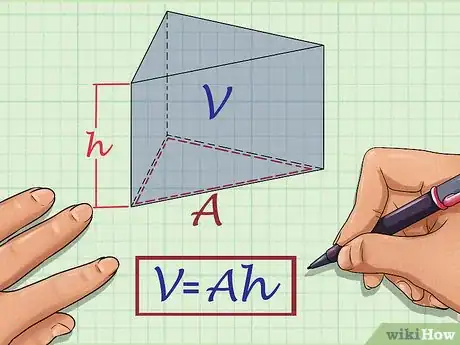
1
Set up the formula for the volume of a prism. The volume for any prism can be found by using the formula $V=Ah$ $V=Ah$ , where $V$ $V$ equals the volume of the prism, $A$ $A$ equals the area of one base, and $h$ $h$ equals the height of the prism.^{[4]
X
Research source}
- The base of a prism is one of its congruent sides. The base of a triangular prism will be a triangle. The sides will be rectangles.
2
Plug the volume into the formula. If you do not know the volume, you cannot use this method.
- For example, if you know the volume of the prism is 840 cubic meters ( $m^{3}$ ), then your formula will look like this:
  $840=Ah$
3
Find the area of the base. To find the area, you need to know the length of the triangle’s base and the height of the triangle. Use the formula $A={\frac {1}{2}}(b)(h)$ $A={\frac {1}{2}}(b)(h)$ to find the area of a triangle.^{[5]
X
Research source}
- Alternatively, if you know the length of all three sides of a triangle, you can find the area using Heron’s formula. ^{[6]
  X
  Research source} Read Calculate the Area of a Triangle for complete instructions.
- For example, if the base of the triangle is 12 meters, and the height of the triangle is 7 meters, to find the area you would calculate:
  $A={\frac {1}{2}}(12)(7)$
  $A={\frac {1}{2}}(84)$
  $A=42$
4
Plug the area of the base into the volume of a prism formula. Make sure you are substituting for the variable $A$ $A$ .
- For example, if you found the area of the base to be 42 square meters, then your formula will look like this:
  $840=42h$
5
Solve the equation for $h$ . This will give you the height of your prism.
- For example, if your equation is $840=42h$ , you would need to divide each side by 42 to find $h$ .Thus:
  ${\frac {840}{42}}={\frac {42h}{42}}$
  $20=h$
- So, the height of your triangular prism would be 20 meters.

Method 3

Method 3 of 4:

Finding the Height of a Rectangular Prism Using Surface Area

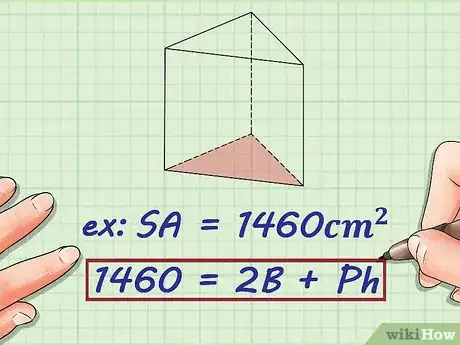
1
Set up the formula for the surface area of a prism. The formula for the surface area of any prism is $SA=2B+Ph$ $SA=2B+Ph$ , where $SA$ $SA$ equals the surface area, $B$ $B$ equals the area of the base, $P$ $P$ equals the perimeter of the base, and $h$ $h$ equals the height of the prism.
- In order for this method to work you must know the surface area of the prism, as well as the length and width of the base.
2
Plug the surface area of the prism into the formula. If you do not know the surface area, this method will not work.
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
  $1460=2B+Ph$
3
Find the area of the base. To find the area, you need to know the length and width of the base (or of one side, if the base is a square). Use the formula $A=lw$ $A=lw$ . To find the area of a rectangle.^{[7]
X
Research source}
- For example, if the base is a rectangle with a length of 8 centimeters and a width of 2 centimeters, to find the area you would calculate:
  $A=(8)(2)$
  $A=16$
4
Plug the area of the base into the formula for the surface area of a prism and simplify. Make sure you are substituting for the letter $B$ $B$ .
- For example, if you found the area of the base to be 16, your formula will look like this:
  $1460=2(16)+Ph$
  $1460=32+Ph$
5
Find the perimeter of the base. To find the perimeter of a rectangle, add up the length of all four sides, or, for a square, multiply the length of one side by 4.
- Remember that opposite sides of a rectangle have the same length. ^{[8]
  X
  Research source}
- For example, if the base is a rectangle with a length of 8 centimeters and a width of 2 centimeters, to find the perimeter you would calculate:
  $P=8+2+8+2$
  $P=20$
6
Plug the perimeter of the base into the formula for the surface area of a prism. Make sure you are substituting for the letter $P$ $P$ .
- For example, if you found the perimeter of the base to be 20, your formula will look like this:
  $1460=32+20h$
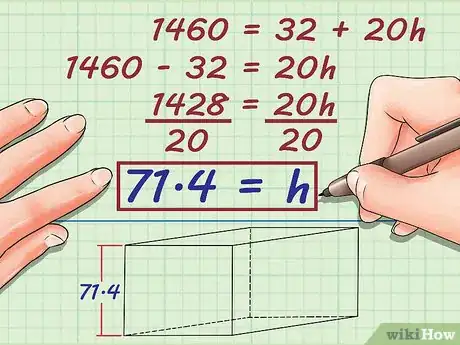
7
Solve the equation for $h$ . This will give you the height of your prism.
- For example, if your equation is $1460=32+20h$ , you would first need to subtract 32 from each side, then divide each side by 20. Thus:
  $1460=32+20h$
  $1428=20h$
  ${\frac {1428}{20}}={\frac {20h}{20}}$
  $71.4=h$
- So, the height of your prism is 71.4 centimeters.

Method 4

Method 4 of 4:

Finding the Height of a Triangular Prism Using Surface Area

1
Set up the formula for the surface area of a prism. The formula for the surface area of any prism is $SA=2B+Ph$ $SA=2B+Ph$ , where $SA$ $SA$ equals the surface area, $B$ $B$ equals the area of the base, $P$ $P$ equals the perimeter of the base, and $h$ $h$ equals the height of the prism.
- In order for this method to work you must know the surface area of the prism, as well as the area of the triangular base, and the length of all three sides of the base.
2
Plug the surface area of the prism into the formula. If you do not know the surface area, this method will not work.
- For example, if you know the surface area is 1460 square centimeters, your formula will look like this:
  $1460=2B+Ph$
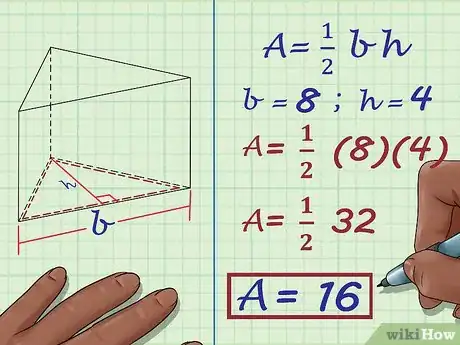
3
Find the area of the base. To find the area, you need to know the length of the triangle’s base and the height of the triangle. Use the formula $A={\frac {1}{2}}(b)(h)$ $A={\frac {1}{2}}(b)(h)$ . To find the area of a triangle.^{[9]
X
Research source}
- Alternatively, if you know the length of all three sides of a triangle, you can find the area using Heron’s formula. ^{[10]
  X
  Research source} Read Calculate the Area of a Triangle for complete instructions.
- For example, if the base of the triangle is 8 centimeters, and the height of the triangle is 4 centimeters, to find the area you would calculate:
  $A={\frac {1}{2}}(8)(4)$
  $A={\frac {1}{2}}(32)$
  $A=16$
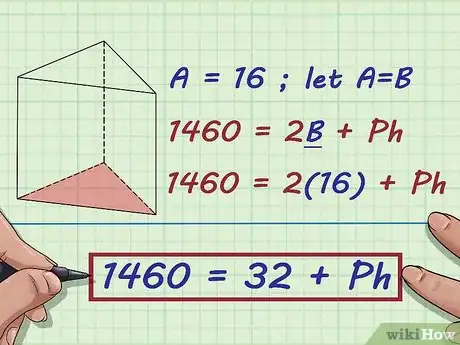
4
Plug the area of the base into the formula for the surface area of a prism and simplify. Make sure you are substituting for the letter $B$ $B$ .
- For example, if you found the area of the base to be 16, your formula will look like this:
  $1460=2(16)+Ph$
  $1460=32+Ph$
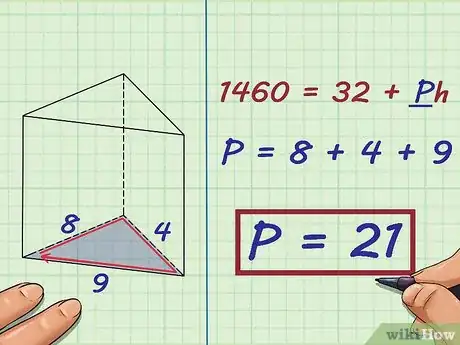
5
Find the perimeter of the base. To find the perimeter of a triangle, add up the length of all three sides.
- For example, if the base is a triangle has three sides with lengths of 8, 4, and 9 centimeters, to find the perimeter you would calculate:
  $P=8+4+9$
  $P=21$
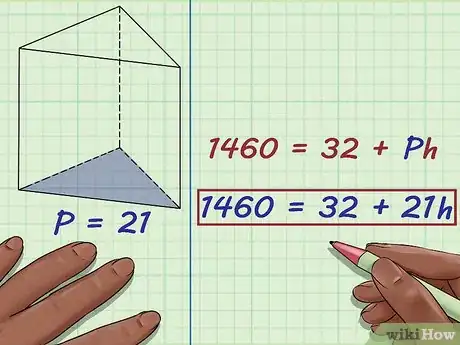
6
Plug the perimeter of the base into the formula for the surface area of a prism. Make sure you are substituting for the letter $P$ $P$ .
- For example, if you found the perimeter of the base to be 21, your formula will look like this:
  $1460=32+21h$
7
Solve the equation for $h$ . This will give you the height of your prism.
- For example, if your equation is $1460=32+21h$ , you would first need to subtract 32 from each side, then divide each side by 21. Thus:
  $1460=32+21h$
  $1428=21h$
  ${\frac {1428}{21}}={\frac {21h}{21}}$
  $68=h$
- So, the height of your prism is 68 centimeters.

Community Q&A

Question

How do I find the height of a cylinder given the volume?

Community Answer

You can use Method 1 and the formula V = Ah. The base of a cylinder is a circle, so A will equal the area of the circle, which is pi x r^2. As long as you know the radius of the circle, you should be able to solve for h.
Question

How can I find the height of a rectangular prism with the width, length and area of base?

Donagan

Top Answerer

You also need to know the volume, in which case, you would divide the volume by the area.
Question

How do I find the width of a rectangular prism?

Donagan

Top Answerer

Assuming you know the volume, divide the volume by the height, then divide by the length.