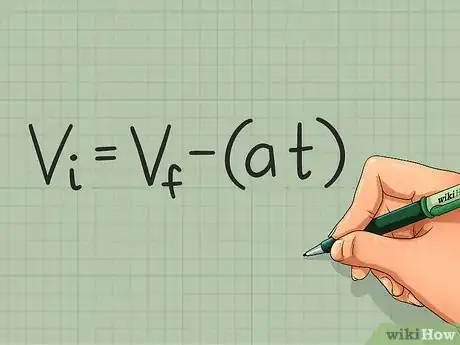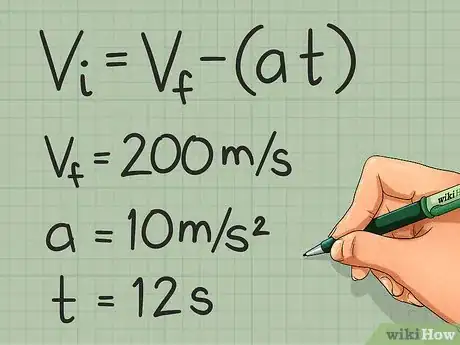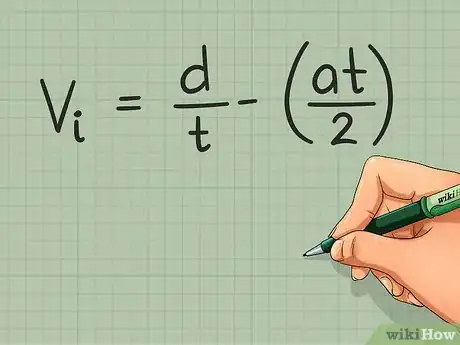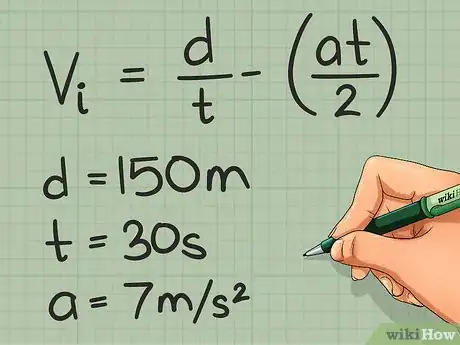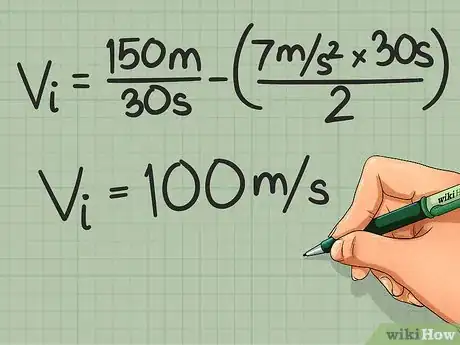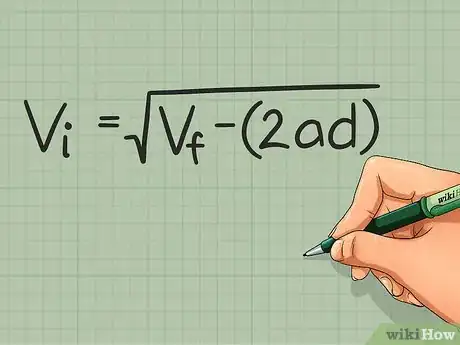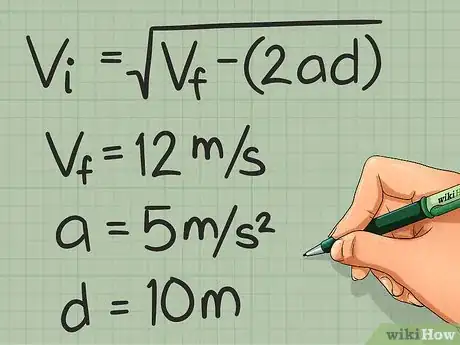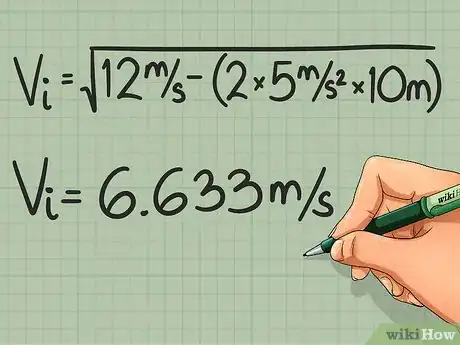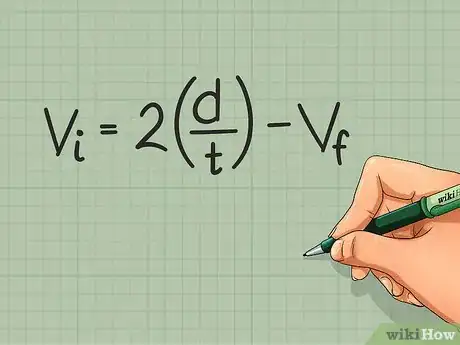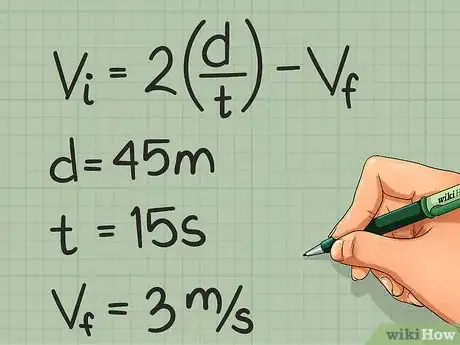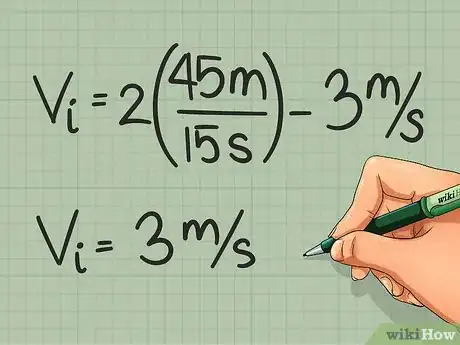How to Find Initial Velocity

Velocity is a function of time and defined by both a magnitude and a direction. [1] Often in physics problems, you will need to calculate the initial velocity (speed and direction) at which an object in question began to travel. There are multiple equations that can be used to determine initial velocity. Using the information given in a problem, you can determine the proper equation to use and easily answer your question.

Method 1
Method 1 of 4:

Finding Initial Velocity with Final Velocity, Acceleration, and Time[2]

  1. Image titled Find Initial Velocity Step 1
    1
    Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you have values for the final velocity, acceleration, and time involved, you can use the following equation:[3]
    • Initial velocity: Vi = Vf - (a * t)
    • Understand what each symbol stands for.
      • Vi stands for “initial velocity”
      • Vf stands for “final velocity”
      • a stands for “acceleration”
      • t stands for “time”
    • Note that this equation is the standard equation used when finding initial velocity.
  2. Image titled Find Initial Velocity Step 2
    2
    Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
    • If you make a mistake, you can easily find it by looking back at all of your previous steps.
    Advertisement
  3. Image titled Find Initial Velocity Step 3
    3
    Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.[4]
    • For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
      • Write the known information:
      • Vi = ?, Vf = 200 m/s, a = 10 m/s2, t = 12 s
    • Multiply the acceleration and time. a * t = 10 * 12 =120
    • Subtract the product from the final velocity. Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 m/s east
    • Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
    4. Advertisement
Method 2
Method 2 of 4:

Finding Initial Velocity with Distance, Time, and Acceleration

  1. Image titled Find Initial Velocity Step 4
    1
    Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation.[5] If you know values for the distance, time, and acceleration, you can use the following equation:
    • Initial velocity: Vi = (d / t) - [(a * t) / 2]
    • Understand what each symbol stands for.
      • Vi stands for “initial velocity”
      • d stands for “distance”
      • a stands for “acceleration”
      • t stands for “time”
  2. Image titled Find Initial Velocity Step 5
    2
    Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
    • If you make a mistake, you can easily find it by looking back at all of your previous steps.
  3. Image titled Find Initial Velocity Step 6
    3
    Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
    • For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
      • Write the known information:
      • Vi = ?, d = 150 m, a = 7 m/s2, t = 30 s
    • Multiply the acceleration and time. a * t = 7 * 30 = 210
    • Divide the product by two. (a * t) / 2 = 210 / 2 = 105
    • Divide the distance by the time. d / t = 150 / 30 = 5
    • Subtract your first quotient from the second quotient. Vi = (d / t) - [(a * t) / 2] = 5 – 105 = -100 Vi = -100 m/s west
    • Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
    4. Advertisement
Method 3
Method 3 of 4:

Finding Initial Velocity with Final Velocity, Acceleration, and Distance [6]

  1. Image titled Find Initial Velocity Step 7
    1
    Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, acceleration, and distance, you can use the following equation:[7]
    • Initial velocity: Vi = √ [Vf2 - (2 * a * d)]
    • Understand what each symbol stands for.
      • Vi stands for “initial velocity”
      • Vf stands for “final velocity”
      • a stands for “acceleration”
      • d stands for “distance”
  2. Image titled Find Initial Velocity Step 8
    2
    Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
    • If you make a mistake, you can easily find it by looking back at all of your previous steps.
  3. Image titled Find Initial Velocity Step 9
    3
    Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
    • For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object's initial velocity.
      • Write the known information:
      • Vi = ?, Vf = 12 m/s, a = 5 m/s2, d = 10 m
    • Square the final velocity. Vf2= 122 = 144
    • Multiply the acceleration by the distance and the number two. 2 * a * d = 2 * 5 * 10 = 100
    • Subtract this product from your previous one. Vf2 - (2 * a * d) = 144 – 100 = 44
    • Take the square root of your answer. = √ [Vf2 - (2 * a * d)] = √44 = 6.633 Vi = 6.633 m/s north
    • Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
    4. Advertisement
Method 4
Method 4 of 4:

Finding Initial Velocity with Final Velocity, Time, and Distance [8]

  1. Image titled Find Initial Velocity Step 10
    1
    Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, time, and distance, you can use the following equation:[9]
    • Initial velocity: Vi = 2(d/t) - Vf
    • Understand what each symbol stands for.
      • Vi stands for “initial velocity”
      • Vf stands for “final velocity”
      • t stands for “time”
      • d stands for “distance”
  2. Image titled Find Initial Velocity Step 11
    2
    Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
    • If you make a mistake, you can easily find it by looking back at all of your previous steps.
  3. Image titled Find Initial Velocity Step 12
    3
    Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
    • For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object's initial velocity.
      • Write the known information:
      • Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m
    • Divide distance by time. (d/t) = (45/15) = 3
    • Multiply that value by 2. 2 (d/t) = 2 (45/15) = 6
    • Subtract final velocity from the product. 2(d/t) - Vf = 6 - 3 = 3 Vi = 3 m/s south
    • Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
    4. Advertisement

Community Q&A

  • Question
    A bullet of 60 gm is fired using a rifle of mass 12kg. Rifle recoils with a velocity of 2.5m/s. What is the initial velocity?
    Community Answer
    Community Answer
    Kinetic energy -> Kinetic energy 0.5mv^2 -> 0.5mv^2 0.5 x 12 x 2,5^2 = 0.5 x 0.06 x v^2 6 x 6.25 = 0.03 x v^2 37.5 = 0.03 x v^2 sqrt(37.5/0.03) = v sqrt(1250) = v v = 35.3 m/s
  • Question
    If displacement and time are related as s = 3.5t + 5t2, what is the initial velocity?
    Community Answer
    Community Answer
    Initial velocity is 3.5. The equation is s = ut + 1/2at^2, where s - distance, u - inititial velocity, and a - acceleration.
  • Question
    How do I modify the acceleration formula to one that gives me initial velocity?
    Community Answer
    Community Answer
    You can't change the acceleration formula to one that gives you the initial velocity you want, as a=v/t. However, Vf=Vi+a.t is re-arranged. Vi=Vf-a.t, a=Vf-Vi/t, t=Vf-Vi/a.
Advertisement

Things You'll Need

  • Pencil
  • Paper
  • Calculator (optional)

You Might Also Like

Calculate Speed in Metres per Second
How to
Calculate Speed in Metres per Second
Calculate Tension in Physics
How to
Calculate Tension in Physics
Calculate Acceleration
How to
Calculate Acceleration
Calculate Weight from MassHow Find the Weight of an Object Using Mass and Gravity
Calculate Force
How to
Calculate Force
Calculate Velocity
How to
Calculate Velocity
Calculate Kinetic Energy
How to
Calculate Kinetic Energy
Calculate Mass
How to
Calculate Mass
Calculate Speed
How to
Calculate Speed
Calculate Average Speed
How to
Calculate Average Speed
Calculate Instantaneous Velocity
How to
Calculate Instantaneous Velocity
Calculate Torque
How to
Calculate Torque
Calculate Displacement
How to
Calculate Displacement
Find Normal Force
How to
Find Normal Force
Advertisement

References

  1. ↑ http://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity
  2. ↑ http://easycalculation.com/physics/classical-physics/constant-acc-velocity.php
  3. ↑ https://www.softschools.com/formulas/physics/initial_velocity_formula/81/
  4. ↑ https://www.softschools.com/formulas/physics/initial_velocity_formula/81/
  5. ↑ https://www.omnicalculator.com/physics/velocity
  6. ↑ http://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations
  7. ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion/kinematic-formulas/a/what-are-the-kinematic-formulas
  8. ↑ http://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations
  9. ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion/kinematic-formulas/a/what-are-the-kinematic-formulas

About This Article

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 9 people, some anonymous, worked to edit and improve it over time. This article has been viewed 824,029 times.
140 votes - 57%
Co-authors: 9
Updated: September 16, 2022
Views: 824,029
Categories: Classical Mechanics
Article SummaryX

To find initial velocity, start by multiplying the acceleration by the time. Then, divide that number by 2 and write down the quotient you get. Next, divide the distance by the time and write down that quotient as well. Finally, subtract your first quotient from your second quotient to find the initial velocity. To learn how to find initial velocity using the final velocity, keep reading!

Did this summary help you?
Advertisement