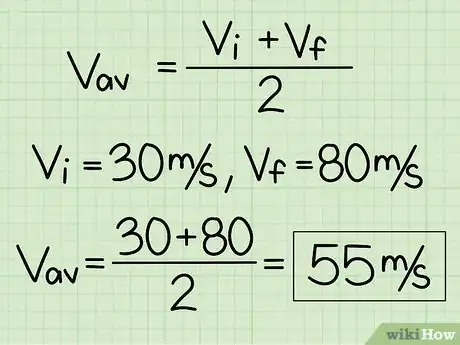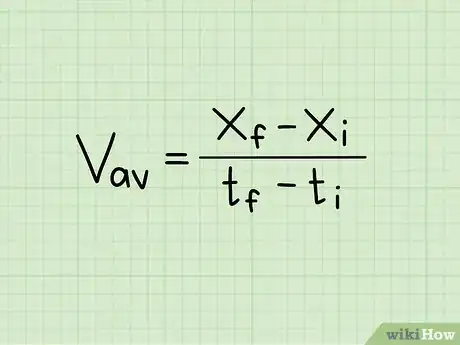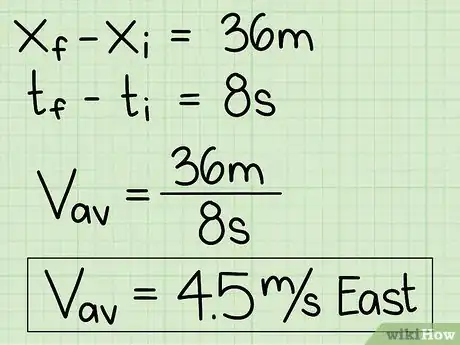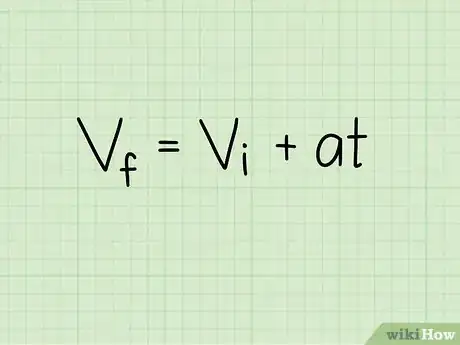How to Calculate Velocity

Co-authored by Sean Alexander, MS

Velocity is an object's speed in a particular direction. Mathematically, velocity is often described as the change in position over the change in time.^{[1]
X
Expert Source

Sean Alexander, MS
Academic Tutor
Expert Interview. 14 May 2020.}^{[2]
X
Research source} This fundamental concept shows up in many basic physics problems. Which formula you use depends on what you know about the object, so read carefully to make sure you've chosen the right one.

Quick Formulas

Average velocity = $v_{av}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ $v_{{av}}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$
- $x_{f}=$ final position $x_{i}=$ initial position
- $t_{f}=$ final time $t_{i}=$ initial time
Average velocity if acceleration is constant = $v_{av}={\frac {v_{i}+v_{f}}{2}}$ $v_{{av}}={\frac {v_{i}+v_{f}}{2}}$
- $v_{i}=$ initial velocity $v_{f}=$ final velocity
Average velocity if acceleration is zero and constant = $v_{av}={\frac {x}{t}}$
Final velocity = $v_{f}=v_{i}+at$ $v_{f}=v_{i}+at$
- a = acceleration t = time

Method 1

Method 1 of 3:

Finding Average Velocity

1
Find average velocity when acceleration is constant. If an object is accelerating at a constant rate, the formula for average velocity is simple:^{[3]
X
Research source} $v_{av}={\frac {v_{i}+v_{f}}{2}}$ $v_{{av}}={\frac {v_{i}+v_{f}}{2}}$ . In this equation $v_{i}$ $v_{i}$ is the initial velocity, and $v_{f}$ $v_{f}$ is the final velocity. Remember, you can only use this equation if there is no change in acceleration.
- As a quick example, let's say a train accelerates at a constant rate from 30 m/s to 80 m/s. The average velocity of the train during this time is ${\frac {30+80}{2}}=55m/s$ .
2
Set up an equation with position and time instead. You can also find the velocity from the object's change in position and time. This works for any problem. Note that, unless the object is moving at a constant velocity, your answer will be the average velocity during the movement, not the specific velocity at a certain time.^{[4]
X
Research source}
- The formula for this problem is $v_{av}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ , or "final position - initial position divided by final time - initial time." You can also write this as $v_{av}$ = ^Δx / _Δt, or "change in position over change in time."
Advertisement
3
Find the distance between the start and end points. When measuring velocity, the only positions that matter are where the object started, and where the object ended up. This, along with which direction the object traveled, tells you the displacement, or change in position.^{[5]
X
Research source} The path the object took between these two points does not matter.
- Example 1: A car traveling due east starts at position x = 5 meters. After 8 seconds, the car is at position x = 41 meters. What was the car's displacement?
  - The car was displaced by (41m - 5m) = 36 meters east.
- Example 2: A diver leaps 1 meter straight up off a diving board, then falls downward for 5 meters before hitting the water. What is the diver's displacement?
  - The diver ended up 4 meters below the starting point, so her displacement is 4 meters downward, or -4 meters. (0 + 1 - 5 = -4). Even though the diver traveled six meters (one up, then five down), what matters is that the end point is four meters below the start point.
4
Calculate the change in time. How long did the object take to reach the end point? Many problems will tell you this directly. If it does not, subtract the start time from the end time to find out.^{[6]
X
Research source}
- Example 1 (cont.): The problem tells us that the car took 8 seconds to go from the start point to the end point, so this is the change in time.
- Example 2 (cont.): If the diver jumped at t = 7 seconds and hits the water at t = 8 seconds, the change in time = 8s - 7s = 1 second.
5
Divide the total displacement by the total time. In order to find the velocity of the moving object, you will need to divide the change in position by the change in time. Specify the direction moved, and you have the average velocity.^{[7]
X
Research source}
- Example 1 (cont.): The car changed its position by 36 meters over 8 seconds. $v_{av}={\frac {36m}{8s}}=$ 4.5 m/s east.
- Example 2 (cont): The diver changed her position by -4 meters over 1 second. $v_{av}={\frac {-4m}{1s}}=$ -4 m/s. (In one dimension, negative numbers are usually used to mean "down" or "left." You could say "4 m/s downward" instead.)
6
Solve problems in two dimensions. Not all word problems involve movement back along one line. If the object turns at some point, you may need to draw a diagram and solve a geometry problem to find the distance.
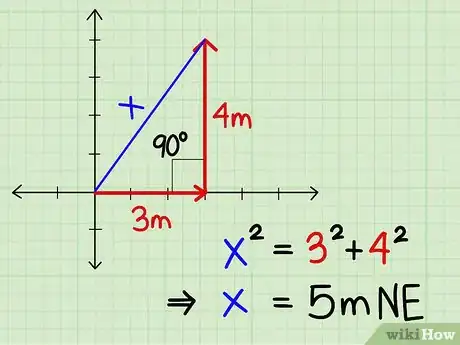
- Example 3: A man jogs for 3 meters east, then make a 90º turn and travels 4 meters north. What is his displacement?
  - Draw a diagram and connect the start point and end point with a straight line. This is the hypotenuse of a triangle, so solve for its length of this line using properties of right triangles. In this case, the displacement is 5 meters northeast.
  - At some point, your math teacher may require you to find the exact direction traveled (the angle above the horizontal). You can do this by using geometry or by adding vectors.

Method 2

Method 2 of 3:

Finding Velocity from Acceleration

1
Understand the velocity formula for an accelerating object. Acceleration is the change in velocity. If the acceleration is constant, the velocity continues to change at the same rate.^{[8]
X
Expert Source

Sean Alexander, MS
Academic Tutor
Expert Interview. 14 May 2020.}We can describe this by multiplying acceleration and time, and adding the result to the initial velocity:
- $v_{f}=v_{i}+at$ , or "final velocity = initial velocity + (acceleration * time)"
- Initial velocity $v_{i}$ is sometimes written as $v_{0}$ ("velocity at time 0").
2
Multiply the acceleration by the change in time. This will tell you how much the velocity increased (or decreased) over this time period.^{[9]
X
Research source}
- Example: A ship sailing north at 2 m/s accelerates north at a rate of 10 m/s². How much did the ship's velocity increase in the next 5 seconds?
  - a = 10 m/s²
  - t = 5 s
  - (a * t) = (10 m/s² * 5 s) = 50 m/s increase in velocity.
3
Add the initial velocity. Now you know the total change in the velocity. Add this to the initial velocity of the object, and you have your answer.^{[10]
X
Research source}
- Example (cont): In this example, how fast is the ship traveling after 5 seconds?
  - $v_{f}=v_{i}+at$
  - $v_{i}=2m/s$
  - $at=50m/s$
  - $v_{f}=2m/s+50m/s=52m/s$
4
Specify the direction of movement. Unlike speed, velocity always includes the direction of movement. Make sure to include this in your answer.
- In our example, since the ship started going north and did not change direction, its final velocity is 52 m/s north.
5
Solve related problems. As long as you know the acceleration, and the velocity at any one point in time, you can use this formula to find the velocity at any other time. Here's an example solving for the initial velocity:
- "A train accelerates at 7 m/s² for 4 seconds, and ends up traveling forward at a velocity of 35 m/s. What was its initial velocity?"
  - $v_{f}=v_{i}+at$
    $35m/s=v_{i}+(7m/s^{2})(4s)$
    $35m/s=v_{i}+28m/s$
    $v_{i}=35m/s-28m/s=7m/s$

Method 3

Method 3 of 3:

Circular Velocity

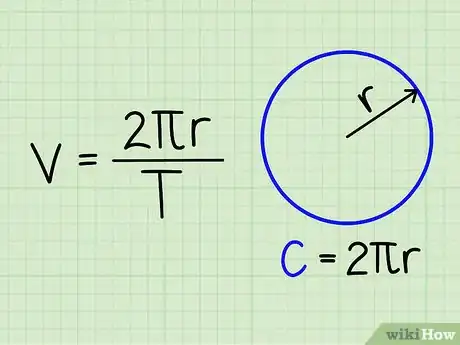
1
Learn the formula for circular velocity. Circular velocity refers to the velocity that one object must travel in order to maintain its circular orbit around another object, usually a planet or other gravitating mass.^{[11]
X
Research source}
- The circular velocity of an object is calculated by dividing the circumference of the circular path by the time period over which the object travels.
- When written as a formula, the equation is:
  - v = ^(2πr) / _T
- Note that 2πr equals the circumference of the circular path.
- r stands for "radius"
- T stands for "time period"
2
Multiply the circular radius by 2π. The first stage of the problem is calculating the circumference. To do this, multiply the radius by 2π. If you are calculating this by hand, you can use 3.14 as an approximation for π.^{[12]
X
Research source}
- Example: Find the circular velocity of an object traveling a circular path with a radius of 8 m over a full time interval of 45 seconds.
  - r = 8 m
  - T = 45 s
  - Circumference = 2πr = ~ (2)(3.14)(8 m) = 50.24 m
3
Divide this product by the time period. In order to find the circular velocity of the object in question, you need to divide the calculated circumference by the time period over which the object traveled.^{[13]
X
Research source}
- Example: v = ^(2πr) / _T = ^{50.24 m} / _{45 s} = 1.12 m/s
  - The circular velocity of the object is 1.12 m/s.

Calculator, Practice Problems, and Answers

Sample Calculating Velocity Calculator

Sample Calculating Velocity Practice Problems

Sample Calculating Velocity Practice Answers

Community Q&A

Question

When do we have deceleration?

Benjamin Walker

Community Answer

As the object loses energy passing through a medium. The medium an object is passing through will determine the deceleration.
Question

How do I calculate the velocity of something given its time traveled and distance covered?

Community Answer

Divide distance traveled by the time taken to get the average speed. Velocity is the term used for speed when the object travels in a uniform direction (i.e. straight line or circle).
Question

How does velocity change if the distance decreases and the time increases?

Community Answer

Velocity decreases. Think about it: It takes a longer time to cover a shorter distance.