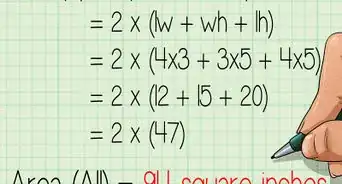This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
There are 11 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 72,464 times.
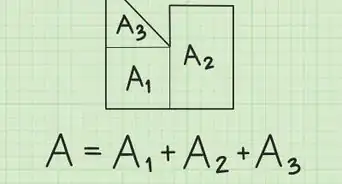
Area is a measurement of the amount of space inside a two-dimensional figure. Sometimes, finding area can be as simple as simply multiplying two numbers, but oftentimes it can be more complicated. Read this article for a brief overview for the following shapes: quadrilaterals, triangles, circles, surface areas of pyramids and cylinders, and the area under an arc.
Steps
Rectangles
-
1Find the lengths of two consecutive sides of the rectangle. Because rectangles have two pairs of sides of equal length, label one side as the base (b) and one side as the height (h). Generally, the horizontal side is the base and the vertical side is the height.[1]
-
2Multiply base times height to get the area. If the area of the rectangle is k, k=b*h. This means that the area is simply the product of the base and the height.[2]
- For more extensive instructions, check out How to Find the Area of a Quadrilateral
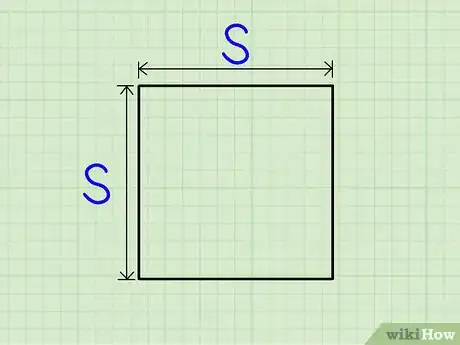
Squares
-
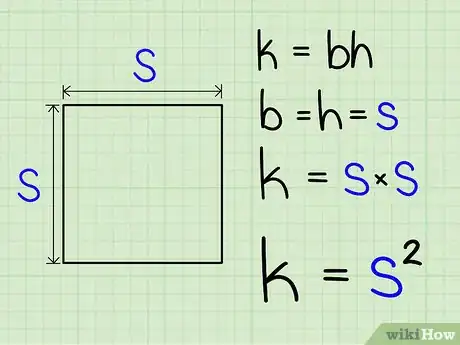
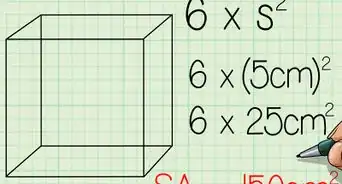
1Find the length of a side of the square. Because squares have four equal sides, all of the sides should have this same measurement.[3]
-
2Square the length of the side. This is your area.[4]
- This works because a square is simply a special rectangle that has equal width and length. So, in solving k=b*h, b and h are both the same value. So, you end up squaring a single number in order to find the area.
Parallelograms
-
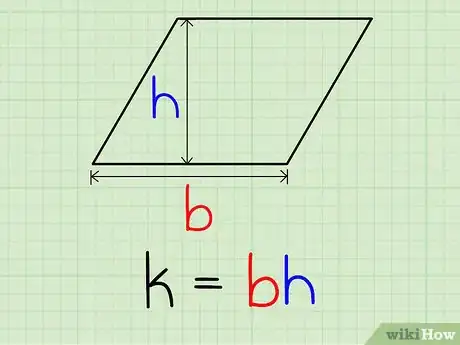
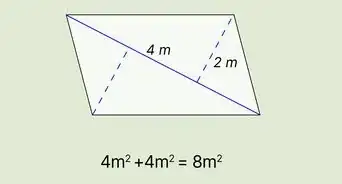
1Choose one side to be the base of the parallelogram. Find the length of this base.
-
2Draw a perpendicular line to this base, and determine the length of this line between where it crosses the base and the side opposite to the base. This length is the height.[5]
- If the side opposite to the base is not long enough that the perpendicular line crosses it, extend the side along the line until it intersects the perpendicular line.
-
3Plug the base and height into the equation k=b*h.[6]
- For more extensive instructions, check out How to Find the Area of a Parallelogram
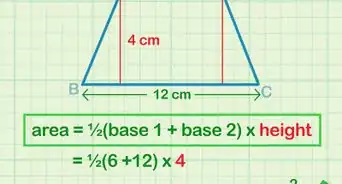
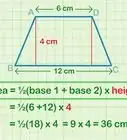
Trapezoids
-
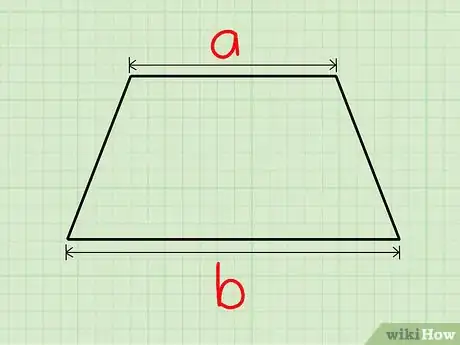
1Find the lengths of the two parallel sides. Assign these values to variables a and b.
-
2Find the height. Draw a perpendicular line that crosses both parallel sides, and the length of the line segment on this line connecting the two sides is the height of the parallelogram (h).[7]
-
3Plug these values into the formula A=0.5(a+b)h.[8]
- For more extensive instructions, check out How to Calculate the Area of a Trapezoid
Triangles
-
1Find the base and height of the triangle. This is the length of one side of the triangle (the base), and the length of the line segment perpendicular to the base connecting the base to the opposite vertex of the triangle.
-
2To find the area, plug the base and height values into the equation A=0.5b*h.[9]
- For more extensive instructions, check out How to Calculate the Area of a Triangle
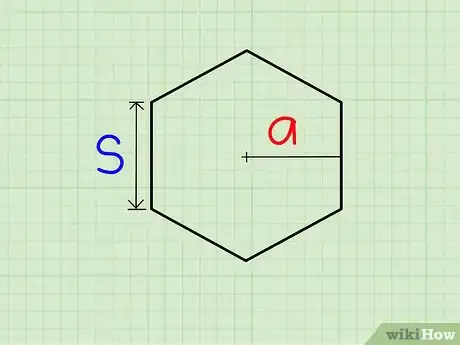
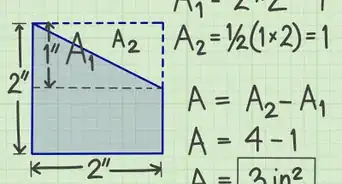
Regular Polygons
-
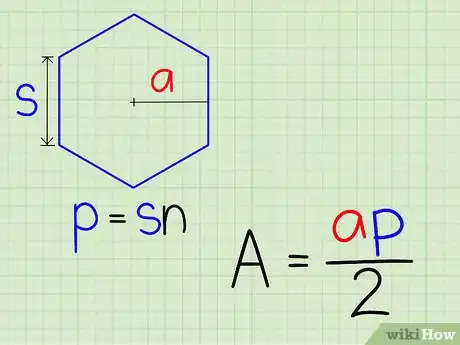
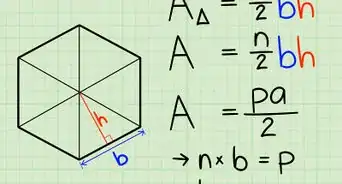
1Find the length of a side and the length of the apothem (the line segment perpendicular to a side connecting the middle of a side to the center. The length of the apothem will be assigned the variable a.
-
2Multiply the length of the side by the number of sides to get the perimeter of the polygon (p).
-
3Plug these values into the equation A=0.5a*p
- For more extensive instructions, check out How to Find the Area of Regular Polygons
Circles
-
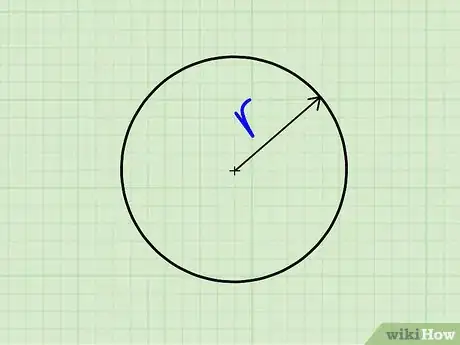
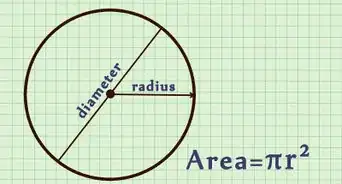
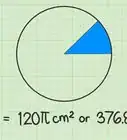
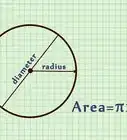
1Find the radius of the circle (r). This is a line segment connecting the center to a point on the circle. By definition, this value is the same no matter what point you pick on the circle.
-
2Plug the radius into the equation A=πr^2.[10]
- For more extensive instructions, check out How to Calculate the Area of a Circle
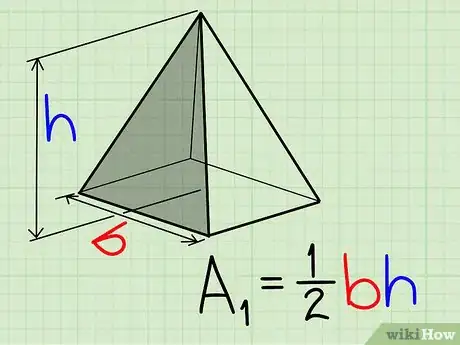
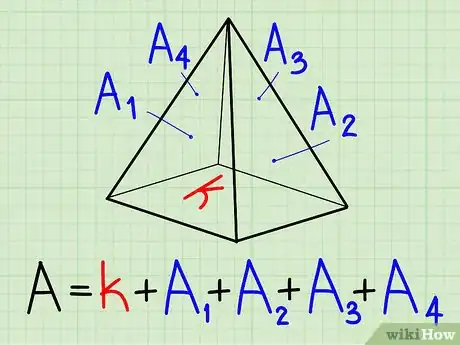
Surface Area of a Pyramid
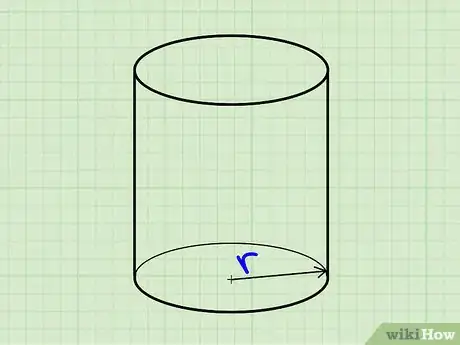
Surface Area of a Cylinder
-
1Find the radius of one of the base circles.
-
2Find the height of the cylinder
-
3Find the area of the bases using the formula of the area of a circle: A=πr^2.[11]
-
4Find the area of the side by multiplying the height of the cylinder by the perimeter of the base. The perimeter of a circle is P=2πr, so the area of the side is A=2πhr.[12]
-
5Add up all the areas: the two identical circular bases and the side. So, the surface area should be SA=2πr^2+2πhr.
- For more extensive instructions, check out How to Find the Surface Area of Cylinders
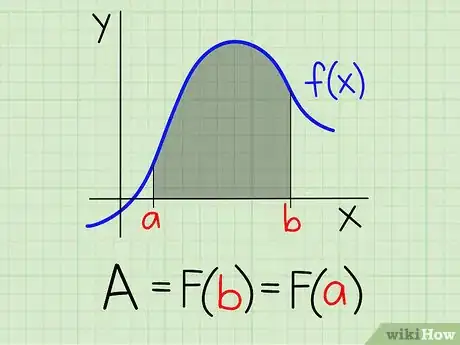
The Area Under a Function
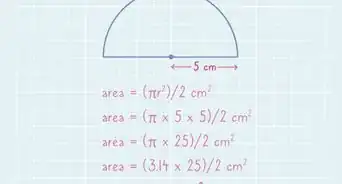
Say you want to find the area under a curve and above the x-axis modeled by function f(x) in the domain interval x within [a,b]. This method requires knowledge of integral calculus. If you have not taken an introductory calculus course, this method may not make any sense.
References
- ↑ https://www.khanacademy.org/math/cc-third-grade-math/imp-geometry/imp-multiply-to-find-area/a/area-rectangles-review
- ↑ David Jia. Academic Tutor. Expert Interview. 7 January 2021.
- ↑ https://www.cuemath.com/measurement/area-of-square/
- ↑ https://www.omnicalculator.com/math/square-area
- ↑ https://www.bbc.com/bitesize/guides/z2mtyrd/revision/5
- ↑ https://www.khanacademy.org/math/cc-sixth-grade-math/x0267d782:cc-6th-plane-figures/cc-6th-parallelogram-area/a/area-of-parallelogram
- ↑ https://www.mathopenref.com/trapezoidarea.html
- ↑ https://www.varsitytutors.com/isee_middle_level_math-help/how-to-find-the-area-of-a-trapezoid
- ↑ https://www.omnicalculator.com/math/triangle-area