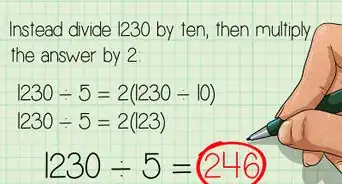How to Teach Decimals

Last Updated: November 18, 2022 References

Decimals can be tricky, so it’s important to break them down step by step. Start by explaining whole number place values, like tens and hundreds. Describe decimals as “in-between” numbers with their own set of place values, including tenths and hundredths. Mention that decimals are related to fractions, and show your students how to convert one to the other. Once you’ve covered the basics, introduce mathematical operations, such as adding and subtracting, that involve decimals.

Method 1

Method 1 of 3:

Explaining Basic Concepts

1
Start by reviewing whole number place values. Write down whole numbers and explain that each number stands for a place value. Show your students which place stands for ones, tens, and hundreds.^{[1]
X
Expert Source

Courtney Copriviza
Elementary School Teacher
Expert Interview. 18 June 2021.}
- For instance, write down 382. Tell students that the number farthest to the right, or 2, stands for ones, the next number to the left, or 8, is the tens place, and the next to the left, or 3, is hundreds.
2
Explain that decimals are “in-between” numbers. Explain that not all numbers are whole numbers. Describe how 5 and 6 are whole numbers, but there are lots of numbers in between them. Show your students how to place a decimal point to the right of the ones place, and mention that numbers after the point are in between 2 whole numbers.^{[2]
X
Research source}
- Write “5.” and say, “If you see another 5 after the point (write ‘5.5’), that means it’s in between 5 and 6.”
Advertisement
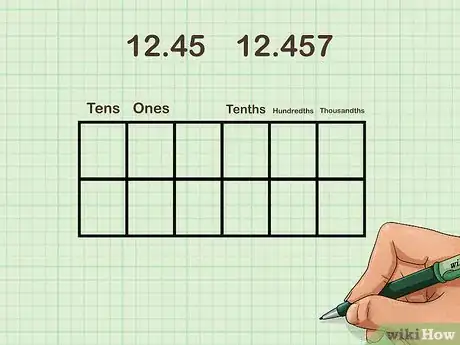
3
Introduce decimal place values. Explain that, like whole numbers, there are place values to the right of a decimal point. Tell students that ones are always immediately to the left of a decimal point. Show them that tenths are always immediately to the right, followed by hundredths and thousandths.^{[3]
X
Research source}
- Over-pronounce tenths and hundredths to avoid confusing decimal place values with tens and hundreds.
4
Describe how fractions and decimals are related. Explain that decimals and fractions are 2 ways of representing “in-between” numbers. Tell learners that fractions can be turned into a decimal that stands for the same number.^{[4]
X
Research source}
- Coloring grids or shapes is helpful. Draw a rectangle, then add lines to divide it into 10 equal strips. Have them color in a strip, then explain that the strip is 1/10 of the rectangle. Tell them that 0.1 is another way of saying 1/10, or one-tenth.
5
Explain how to convert fractions to decimals using division. Write down basic sample fractions, such as 1/4, 1/2, and 3/4. Explain that the fraction means the number on top is divided by the number on the bottom. Show students that dividing the top number, or 1, by the bottom number, or 4, gives you a decimal value, or 0.25.^{[5]
X
Research source}
- Practice using division to convert basic fractions to decimals. Then show how the decimal place values, such as the tenths and hundredths places, relate to the top and bottom numbers of the fraction. For example, 0.25 means 25/100.
6
Practice reading fractions and decimal values out loud. Write down a series of mixed decimal numbers and read them out loud. Teach your students to use the correct place values instead of reading 1.5 as “one point five.”
- Write down 25.45 and read it out loud as “twenty-five and forty-five hundredths.” Write 54.035 and read it as “fifty-four and thirty-five thousandths.”
- After demonstrating how to read decimals, write down several examples and have them read the numbers out loud. If necessary, correct them gently and say, “That’s a great try, but remember this number means thousandths. Give it another shot!”
7
Explain how to see if one number is bigger than another. Describe how place values in whole numbers and decimals differ. Explain that, while hundreds are greater than tens, tenths are greater than hundredths. Line up 2 decimal numbers on top of each other to demonstrate how to find out which one is bigger.
- For instance, write:
  3.535
  3.353
- Explain that they need to look at the tenths place first to find the bigger number. Since 5 is greater than 3, 3.535 is greater than 3.353.
8
Add zeroes to help your students visualize place values. It might be tough for beginners to compare numbers such as 3.5 and 3.350, since 350 looks like it's bigger than 5. Tell your students that they can add zeroes to the right of a decimal to fill in place values. Mention that adding zeroes to the right doesn't change the number's value.
- They might have an easier time seeing that 3.500 is greater than 3.350. Adding zeroes to decimals will also come in handy when it's time to teach addition and subtraction.

Method 2

Method 2 of 3:

Using Visual Aids

1
Fill in grids to visualize decimal values. Grids with 10 and 100 squares are great ways to show what a decimal is and how to compare it with other numbers. Create your own by drawing a rectangle and dividing into 10 strips, and by drawing a square divided into 100 boxes. You can also download and print ready-made grids.^{[6]
X
Research source}
- Explain that the entire rectangle or square stands for 1. Color in 6 of a rectangle’s 10 strips, and say, “We’ve colored 6 out of 10 strips. That’s 0.6 or 6/10 (six-tenths) of the total strips.”
- Color in 25 of a square’s 100 boxes. Say, “We’ve colored 25 out of 100 boxes. That’s 0.25 or 25/100 (twenty-five hundredths) of the total boxes.”
- Find out which decimals are bigger by coloring grids. Color 35 out of 100 boxes, then color 25 of 100 boxes in a second grid. Explain how 35/100 is greater than 25/100, so 0.35 is greater than 0.25.
2
Draw number lines to compare values. Number lines are another useful way to show how decimals are in between whole numbers.^{[7]
X
Expert Source

Courtney Copriviza
Elementary School Teacher
Expert Interview. 18 June 2021.} Make a horizontal line with vertical dashes at either end. Write 5 above the dash on the left and 6 above the dash on the right.^{[8]
X
Research source}
- Make another dash in the center and label it 5.5. Explain that this number is right in the middle between 5 and 6. Ask them where to place dashes for 5.75 and 5.25, then fill in other decimal values along the number line.
3
Use money to explain decimals. Money is a fantastic, tangible way to teach decimals. Explain how coins represent .01, .05, .10, and .25 of your national currency. Pile up different combinations of coins and use them to demonstrate how to add and subtract decimals.

Method 3

Method 3 of 3:

Doing Operations with Decimals

1
Introduce rounding decimals. Explain that they can round decimals by looking to the right of the rounded place value, and that the rounded place value could be tenths, hundredths, and so on. Tell students that they should check if the number to the right of the rounded place value is greater than or equal to 5.^{[9]
X
Research source}
- Write 2.527 and help them round the number to the nearest hundredth. Identify the hundredth place value in 2.527, then show them the number to its right. Since 7 is greater than 5, they can round the number to 2.53. Mention that if the number were 2.522, they’d round it down to 2.52.
- Give them several practice problems after walking them through a couple of examples.
2
Line numbers up on top of each other to add and subtract. Review how to add and subtract whole numbers. Tell your students that adding and subtracting decimals is basically the same as working with whole numbers. Emphasize how important it is to line up the decimal points when adding and subtracting decimals.^{[10]
X
Research source}
- Remind them that they can add zeroes to a decimal to fill in empty place values. They'll have an easier time subtracting 3.350 from 3.500 if they can see all of the place values.
- Write out example problems and help them add and subtract. Then have them work on problems on their own.
3
Move on to multiplying decimals. Review how to multiply whole numbers. Tell your learners that the major difference in multiplying decimals is that they need to add the total decimal places in the numbers they’re multiplying. The product, which is the result of 2 multiplied numbers, must have as many decimal places as that combined total.^{[11]
X
Research source}
- If you multiply 2.5 by 5.5, count the total decimal places, which is 2 (each has 1 decimal place). The product, or 13.75, has to have 2 decimal places. If you multiply 4.55 by 2.25, the product, or 10.2375, has to have 4 decimal places.
- Work with them on a few examples, then have them practice on their own.
4
Shift the decimal point to the right to divide decimals. Review long division using whole numbers before teaching students how to divide decimals. Explain that you move the divisor’s (the number being divided into the other number) decimal point all the way to the right. Then, you move the dividend’s (the number being divided by the other number) decimal point the same number of places to the right.^{[12]
X
Research source}
- If you’re dividing 15.75 by 1.5, place 1.5 on the outside of the long division symbol and 15.75 inside the symbol. Move the outside number’s decimal point all the way to the right to make 15. Since you moved it 1 place, you’ll then move the inside number’s point 1 place to make 157.5.
- Make a decimal point above the long division symbol, and line it up directly over the inside number’s new point (which is now 157.5, not 15.75). Use long division to divide 15 into 157.5, which is 10.5. Stress how important it is to move and line up the decimal points.
5
Create or download practice problems. Doing practice problems is an essential part of learning math. Make your own or download ready-made worksheets from Math.com (http://www.math.com/school/subject1/lessons/S1U1L2GL.html) and other online resources.
- Have students do at least 10 to 15 example problems each for identifying place values, rounding, converting to fractions, adding, subtracting, multiplying, and dividing. Guide them through the first 2 or 3 problems, then have them practice on their own.
- Have patience and offer lots of encouragement when working on practice problems. Decimals can be tricky, so offer gentle corrections and reassure them that they’ll get the hang of it.

Expert Q&A

Question

What are the options I can use to teach addition and subtraction?

Courtney Copriviza
Elementary School Teacher
Courtney Copriviza is an Elementary School Teacher based in Maui, HI. Courtney specializes in elementary education, classroom management, and social and emotional development. She holds a BA in Communication with a minor in Urban Education and an MA in Teaching from Santa Clara University. Courtney has also taught high school in Madrid, Spain. She is a member of Kappa Delta Pi International Honors Society in Education.

Courtney Copriviza

Elementary School Teacher

Expert Answer

You can use manipulatives, visuals, number lines, and mental strategies to teach simple addition and subtraction to students.
Question

Why is it necessary to teach place value in math?

Courtney Copriviza
Elementary School Teacher
Courtney Copriviza is an Elementary School Teacher based in Maui, HI. Courtney specializes in elementary education, classroom management, and social and emotional development. She holds a BA in Communication with a minor in Urban Education and an MA in Teaching from Santa Clara University. Courtney has also taught high school in Madrid, Spain. She is a member of Kappa Delta Pi International Honors Society in Education.

Courtney Copriviza

Elementary School Teacher

Expert Answer

In math, place value helps the children know which ones are tens and which ones are ones.
Question

What is the purpose of a number line?

Courtney Copriviza
Elementary School Teacher
Courtney Copriviza is an Elementary School Teacher based in Maui, HI. Courtney specializes in elementary education, classroom management, and social and emotional development. She holds a BA in Communication with a minor in Urban Education and an MA in Teaching from Santa Clara University. Courtney has also taught high school in Madrid, Spain. She is a member of Kappa Delta Pi International Honors Society in Education.

Courtney Copriviza

Elementary School Teacher

Expert Answer

The number line helps the students to understand the relationship between numbers.