This article was co-authored by wikiHow staff writer, Hannah Madden. Hannah Madden is a writer, editor, and artist currently living in Portland, Oregon. In 2018, she graduated from Portland State University with a B.S. in Environmental Studies. Hannah enjoys writing articles about conservation, sustainability, and eco-friendly products. When she isn’t writing, you can find Hannah working on hand embroidery projects and listening to music.
This article has been viewed 106,998 times.
Learn more...
Traditionally, a radical or irrational number cannot be left in the denominator (the bottom) of a fraction. When a radical does appear in the denominator, you need to multiply the fraction by a term or set of terms that can remove that radical expression. While the use of calculators make rationalizing fractions a bit dated, this technique may still be tested in class.
Steps
Rationalizing a Monomial Denominator
-
1Examine the fraction. A fraction is written correctly when there is no radical in the denominator. If the denominator contains a square root or other radical, you must multiply both the top and bottom by a number that can get rid of that radical. Note that the numerator can contain a radical. Don't worry about the numerator.[1]
- We can see that there is a in the denominator.
-
2Multiply the numerator and denominator by the radical in the denominator. A fraction with a monomial term in the denominator is the easiest to rationalize. Both the top and bottom of the fraction must be multiplied by the same term, because what you are really doing is multiplying by 1.Advertisement
-
3Simplify as needed. The fraction has now been rationalized.[2]
Rationalizing a Binomial Denominator
-
1Examine the fraction. If your fraction contains a sum of two terms in the denominator, at least one of which is irrational, then you cannot multiply the fraction by it in the numerator and denominator.[3]
- To see why this is the case, write an arbitrary fraction where and are irrational. Then the expression contains a cross-term If at least one of and is irrational, then the cross-term will contain a radical.
- Let's see how this works with our example.
- As you can see, there's no way we can get rid of the in the denominator after doing this.
-
2Multiply the fraction by the conjugate of the denominator. The conjugate of an expression is the same expression with the sign reversed.[4] For example, the conjugate of is
- Why does the conjugate work? Going back to our arbitrary fraction multiplying by the conjugate in the numerator and denominator results in the denominator being The key here is that there are no cross-terms. Since both of these terms are being squared, any square roots will be eliminated.
-
3Simplify as needed.[5]
Working with Reciprocals
-
1Examine the problem. If you are asked to write the reciprocal of a set of terms containing a radical, you will need to rationalize before simplifying. Use the method for monomial or binomial denominators, depending on whichever applies to the problem.[6]
-
2Write the reciprocal as it would usually appear. A reciprocal is created when you invert the fraction.[7] Our expression is actually a fraction. It's just being divided by 1.
-
3Multiply by something that can get rid of the radical on the bottom. Remember, you're actually multiplying by 1, so you have to multiply both the numerator and denominator. Our example is a binomial, so multiply the top and bottom by the conjugate.[8]
-
4Simplify as needed.
- Do not be thrown off by the fact that the reciprocal is the conjugate. This is just a coincidence.
Rationalizing Denominators with a Cube Root
-
1Examine the fraction. You can also expect to face cube roots in the denominator at some point, though they are rarer. This method also generalizes to roots of any index.[9]
-
2Rewrite the denominator in terms of exponents. Finding an expression that will rationalize the denominator here will be a bit different because we cannot simply multiply by the radical.[10]
-
3Multiply the top and bottom by something that makes the exponent in the denominator 1. In our case, we are dealing with a cube root, so multiply by Remember that exponents turn a multiplication problem into an addition problem by the property [11]
- This can generalize to nth roots in the denominator. If we have we multiply the top and bottom by This will make the exponent in the denominator 1.
-
4Simplify as needed.[12]
- If you need to write it in radical form, factor out the
Community Q&A
-
QuestionHow do I rationalize with three terms?
 Community AnswerSomething like 1/(1+root2 + root3)? If so, group as 1+(root2 + root3) and multiply through by the "difference of squares conjugate" 1-(root2 + root3). That makes the denominator -4 - root6, which is still irrational, but did improve from two irrational terms to only one. So repeat the same trick by multiplying through by -4+root6 and the denominator is rationalized.
Community AnswerSomething like 1/(1+root2 + root3)? If so, group as 1+(root2 + root3) and multiply through by the "difference of squares conjugate" 1-(root2 + root3). That makes the denominator -4 - root6, which is still irrational, but did improve from two irrational terms to only one. So repeat the same trick by multiplying through by -4+root6 and the denominator is rationalized. -
QuestionIn your pictures, what does the point mean?
 DonaganTop AnswererIf you're asking about the dots that are placed between various fractions, those are multiplication signs. For example, in the article's second image we see (7√3) / (2√7), then a dot, then (√7 / √7). That means we multiply the first fraction by the second fraction (numerator times numerator, and denominator times denominator), giving us (7√21) / 14, which simplifies to √21 / 2. (Incidentally, the article shows some other dots that are not between fractions. Those are merely "bullet points.")
DonaganTop AnswererIf you're asking about the dots that are placed between various fractions, those are multiplication signs. For example, in the article's second image we see (7√3) / (2√7), then a dot, then (√7 / √7). That means we multiply the first fraction by the second fraction (numerator times numerator, and denominator times denominator), giving us (7√21) / 14, which simplifies to √21 / 2. (Incidentally, the article shows some other dots that are not between fractions. Those are merely "bullet points.") -
QuestionHow can I rationalize the denominator with a cube root that has a variable?
 Community AnswerIf it is a binomial expression, follow the steps outlined in method 2.
Community AnswerIf it is a binomial expression, follow the steps outlined in method 2.
References
- ↑ https://www.youtube.com/watch?v=GS7q-fUDxmQ
- ↑ https://www.youtube.com/watch?v=GS7q-fUDxmQ
- ↑ https://www.chilimath.com/lessons/intermediate-algebra/rationalizing-the-denominator/
- ↑ https://www.chilimath.com/lessons/intermediate-algebra/rationalizing-the-denominator/
- ↑ https://www.chilimath.com/lessons/intermediate-algebra/rationalizing-the-denominator/
- ↑ https://www.khanacademy.org/math/algebra-home/alg-exp-and-log/miscellaneous-radicals/v/how-to-rationalize-a-denominator
- ↑ https://www.mathsisfun.com/reciprocal.html
- ↑ https://www.khanacademy.org/math/algebra-home/alg-exp-and-log/miscellaneous-radicals/v/how-to-rationalize-a-denominator
- ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut41_rationalize.htm
About This Article
To rationalize a denominator, start by multiplying the numerator and denominator by the radical in the denominator. Then, simplify the fraction if necessary. If you're working with a fraction that has a binomial denominator, or two terms in the denominator, multiply the numerator and denominator by the conjugate of the denominator. To get the conjugate, just reverse the sign in the expression. Then, simplify your answer as needed. To learn how to rationalize a denominator with a cube root, scroll down!



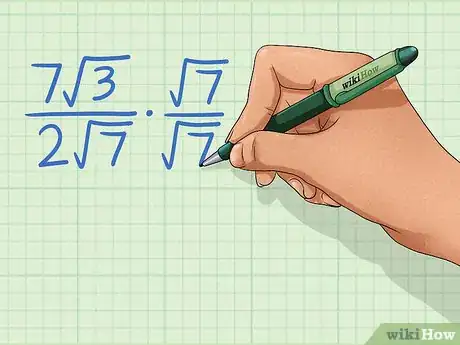

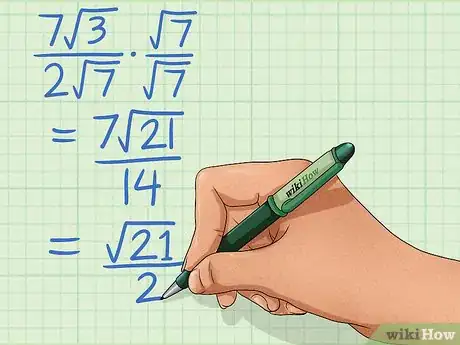














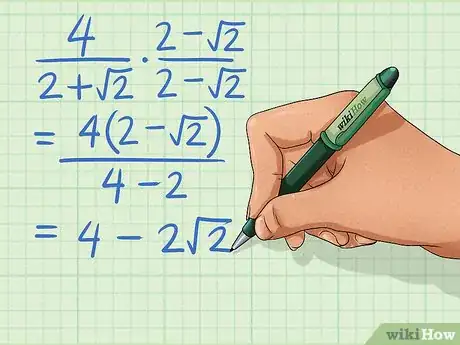

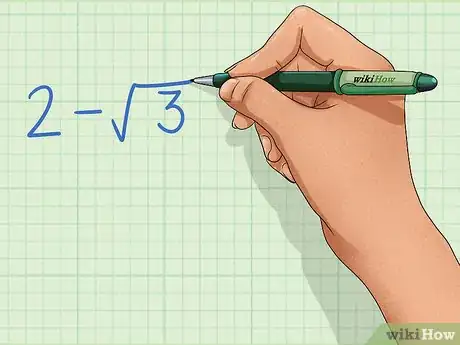

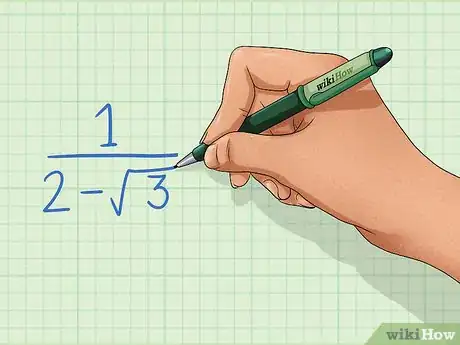

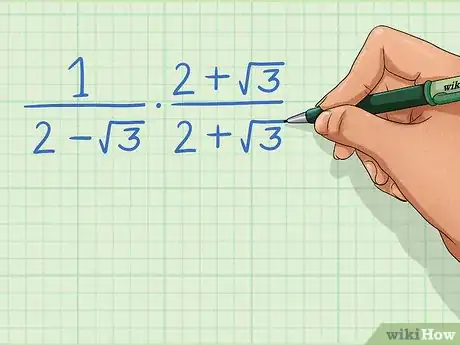




![{\frac {3}{{\sqrt[ {3}]{3}}}}](./images/1927618508-3a37ab9394065e1be3dca1eeb4e96021d86c08a2.webp)











![3^{{2/3}}=(3^{{2}})^{{1/3}}={\sqrt[ {3}]{9}}](./images/1961041752-e059be31ff9a14ad50f7f395de6079811267a674.webp)