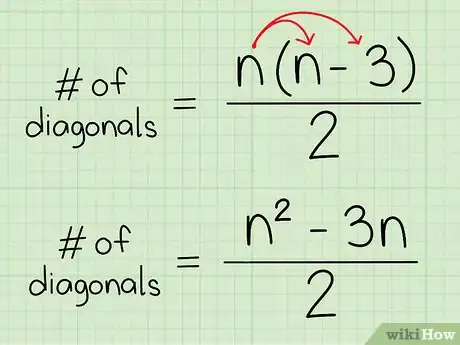How to Find How Many Diagonals Are in a Polygon

Finding diagonals in a polygon is a necessary skill to develop in math. It may seem difficult at first, but is pretty simple once you learn the basic formula. A diagonal is any line segment drawn between vertices of a polygon that doesn’t include the sides of that polygon.[1] A polygon is any shape that has more than three sides. Using a very simple formula, you can calculate the number of diagonals in any polygon, whether it has 4 sides or 4,000 sides.

Method 1
Method 1 of 2:

Drawing the Diagonals

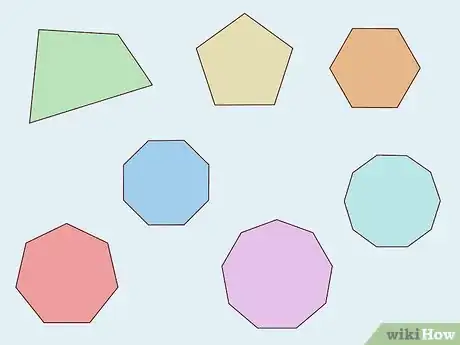
  1. Image titled Find How Many Diagonals Are in a Polygon Step 1
    1
    Know the names of polygons. You may need to first identify how many sides are present in the polygon. Each polygon has a prefix that indicates the number of sides it has. Here are the names of polygons with up to twenty sides:[2]
    • Quadrilateral/tetragon: 4 sides
    • Pentagon: 5 sides
    • Hexagon: 6 sides
    • Heptagon: 7 sides
    • Octagon: 8 sides
    • Nonagon/Enneagon: 9 sides
    • Decagon: 10 sides
    • Hendecagon: 11 sides
    • Dodecagon: 12 sides
    • Triskaidecagon/tridecagon: 13 sides
    • Tetrakaidecagon/tetradecagon: 14 sides
    • Pentadecagon: 15 sides
    • Hexadecagon: 16 sides
    • Heptadecagon: 17 sides
    • Octadecagon: 18 sides
    • Enneadecagon: 19 sides
    • Icosagon: 20 sides
    • Note that a triangle has no diagonals.[3]
  2. Image titled Find How Many Diagonals Are in a Polygon Step 2
    2
    Draw the polygon. If you wanted to know how many diagonals were present in a square, you would start by drawing the square. The easiest way to find diagonals and count them is to draw the polygon symmetrically, each side has the same length. It’s important to note that even if the polygon is not symmetrical, it will still have the same number of diagonals.[4]
    • To draw the polygon, use a ruler and draw each side the same length, connecting all of the sides together.
    • If you’re unsure what the polygon will look like, search for pictures online. For example, a stop sign is an octagon.
    Advertisement
  3. Image titled Find How Many Diagonals Are in a Polygon Step 3
    3
    Draw the diagonals. A diagonal is a line segment drawn from one corner of the shape to another, excluding the sides of the polygon.[5] Starting at one vertex of the polygon, use a ruler to draw a diagonal to every other available vertex.
    • For a square, draw one line from the bottom left corner to the top right corner and another line from the bottom right corner to the top left corner.
    • Draw diagonals in different colors to make them easier to count.
    • Note that this method gets much more difficult with polygons that have more than ten sides.
  4. Image titled Find How Many Diagonals Are in a Polygon Step 4
    4
    Count the diagonals. There are two options for counting: you can count as you draw the diagonals or count them once they have been drawn. As you count each diagonal, draw a small number above the diagonal to denote that it has been counted. It is easy to lose track while counting when there are a lot of diagonals crossing each other.
    • For the square, there are two diagonals: one diagonal for every two vertices.
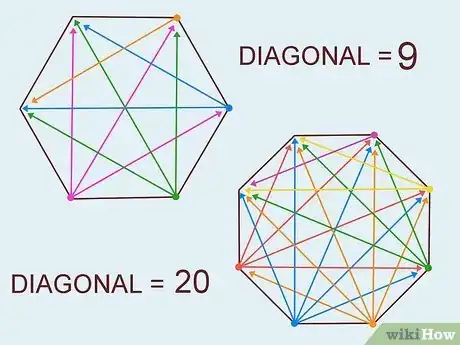
    • A hexagon has 9 diagonals: there are three diagonals for every three vertices.
    • An octagon has 20 diagonals. Past the heptagon, it gets more difficult to count the diagonals because there are so many of them.
  5. Image titled Find How Many Diagonals Are in a Polygon Step 5
    5
    Beware of counting a diagonal more than once. Each vertex may have multiple diagonals, but that doesn’t mean that the number of diagonals is equal to the number of vertices times the number of diagonals. Take care when counting the diagonals to count each one only once.[6]
    • For example, a pentagon (5 sides) has only 5 diagonals. Each vertex has two diagonals, so if you counted each diagonal from every vertex twice, you might think there were 10 diagonals. This is incorrect because you would have counted each diagonal twice!
  6. Image titled Find How Many Diagonals Are in a Polygon Step 6
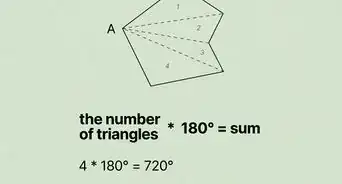
    6
    Practice with some examples. Draw some other polygons and count the number of diagonals. The polygon does not have to be symmetric for this method to work. In the case of a concave polygon, you may have to draw some of the diagonals outside the actual polygon.[7]
    • A hexagon has 9 diagonals.
    • A octagon has 20 diagonals.
    7. Advertisement
Method 2
Method 2 of 2:

Using the Diagonal Formula

  1. Image titled Find How Many Diagonals Are in a Polygon Step 7
    1
    Define the formula. The formula to find the number of diagonals of a polygon is n(n-3)/2 where “n” equals the number of sides of the polygon.[8] Using the distributive property this can be rewritten as (n2 - 3n)/2. You may see it either way, both equations are identical.[9]
    • This equation can be used to find the number of diagonals of any polygon.
    • Note that the triangle is an exception to this rule. Due to the shape of the triangle, it does not have any diagonals.[10]
  2. Image titled Find How Many Diagonals Are in a Polygon Step 8
    2
    Identify the number of sides in the polygon. To use this formula, you must identify the number of sides that the polygon has. The number of sides is given in the name of the polygon, you just need to know what each name means. Here are some of common prefixes you will see in polygons:[11]
    • Tetra (4), penta (5), hexa (6), hepta (7), octa (8), ennea (9), deca (10), hendeca (11), dodeca (12), trideca (13), tetradeca (14), pentadeca (15), etc.
    • For very large sided polygons you may simply see it written “n-gon”, where “n” is the number of sides. For example, a 44-sided polygon would be written as 44-gon.
    • If you are given a picture of the polygon, you can simply count the number of sides.
  3. Image titled Find How Many Diagonals Are in a Polygon Step 9
    3
    Plug the number of sides into the equation.[12] Once you know how many sides the polygon has, you just need to plug that number into the equation and solve. Everywhere you see “n” in the equation will be replaced with the number of sides of the polygon.[13]
    • For example: A dodecagon has 12 sides.
    • Write the equation: n(n-3)/2
    • Plug in the variable: (12(12 - 3))/2
  4. Image titled Find How Many Diagonals Are in a Polygon Step 10
    4
    Solve the equation. Finish by solving the equation using the proper order of operations. Start by solving the subtraction, then multiply, then divide. The final answer is the number of diagonals the polygon has.[14]
    • For example: (12(12 – 3))/2
    • Subtract: (12*9)/2
    • Multiply: (108)/2
    • Divide: 54
    • A dodecagon has 54 diagonals.
  5. Image titled Find How Many Diagonals Are in a Polygon Step 11
    5
    Practice with more examples. The more practice you have with a math concept, the better you will be at using it. Doing lots of examples will also help you memorize the formula in case you need it for a quiz, test, or exam. Remember, this formula works for a polygon of any number of sides greater than 3.[15]
    • Hexagon (6 sides): n(n-3)/2 = 6(6-3)/2 = 6*3/2 = 18/2 = 9 diagonals.
    • Decagon (10 sides): n(n-3)/2 = 10(10-3)/2 = 10*7/2 = 70/2 = 35 diagonals.
    • Icosagon (20 sides): n(n-3)/2 = 20(20-3)/2 = 20*17/2 = 340/2 = 170 diagonals.
    • 96-gon (96 sides): 96(96-3)/2 = 96*93/2 = 8928/2 = 4464 diagonals.
    6. Advertisement

Expert Q&A
Did you know you can get expert answers for this article? Unlock expert answers by supporting wikiHow

  • Question
    What is the formula to find the number of diagonals?
    Jake Adams
    Jake Adams
    Academic Tutor & Test Prep Specialist
    Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
    Jake Adams
    Jake Adams
    Academic Tutor & Test Prep Specialist
    Expert Answer

    Support wikiHow by unlocking this expert answer.

    The basic formula to find the number of diagonals in a polygon is n(n-3)/2.
  • Question
    How many diagonals can be drawn from one vertex of nonagon?
    Community Answer
    Community Answer
    You can draw six, one for each of the vertices, except for the vertex you're drawing from, and the two adjacent vertices.
  • Question
    What is the relationship between the number of sides in an icosikaipentagon and the number of diagonals?
    Donagan
    Donagan
    Top Answerer
    It is the same relationship for any polygon, as expressed in the formula n(n-3)/2.
Advertisement

You Might Also Like

Calculate the Diameter of a Circle
How to
Calculate the Diameter of a Circle
Calculate the Circumference of a Circle
How to
Calculate the Circumference of a Circle
Find the Height of a Triangle
How to
Find the Height of a Triangle
Find Arc Length2 Different Ways to Find a Circle’s Arc Length
Calculate Angles
How to
Calculate Angles
Calculate the Radius of a Circle
How to
Calculate the Radius of a Circle
Find the Center of a Circle
How to
Find the Center of a Circle
Visualize Square Feet
How to
Visualize Square Feet
Determine if Three Side Lengths Are a Triangle
How to
Determine if Three Side Lengths Are a Triangle
How to
Use a Protractor
Measure an Angle Without a Protractor
How to
Measure an Angle Without a Protractor
Find Area and Perimeter
How to
Find Area and Perimeter
Find the Perimeter of a Shape
How to
Find the Perimeter of a Shape
Calculate the Sum of Interior Angles
How to
Calculate the Sum of Interior Angles
Advertisement

References

  1. ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
  2. ↑ https://www.mathsisfun.com/geometry/polygons.html
  3. ↑ https://www.cuemath.com/geometry/diagonals/
  4. ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
  5. ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
  6. ↑ http://www.mathopenref.com/polygondiagonal.html
  7. ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
  8. ↑ Jake Adams. Academic Tutor & Test Prep Specialist. Expert Interview. 20 May 2020.
  9. ↑ https://www.cuemath.com/diagonal-of-a-polygon-formula/
  1. ↑ https://www.cuemath.com/geometry/diagonals/
  2. ↑ http://www.infoplease.com/ipa/A0881983.html
  3. ↑ Jake Adams. Academic Tutor & Test Prep Specialist. Expert Interview. 20 May 2020.
  4. ↑ http://www.mathopenref.com/polygondiagonal.html
  5. ↑ http://www.mathopenref.com/polygondiagonal.html
  6. ↑ https://www.brightstorm.com/math/geometry/reasoning-diagonals-angles-and-parallel-lines/number-of-diagonals-in-a-polygon/

About This Article

Jake Adams
Co-authored by:
Jake Adams
Academic Tutor & Test Prep Specialist
This article was co-authored by Jake Adams. Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University. This article has been viewed 351,762 times.
36 votes - 66%
Co-authors: 21
Updated: January 31, 2023
Views: 351,762
Categories: Geometry | Mathematics
Article SummaryX

To find out how many diagonals a polygon has, first count the number of sides, or straight lines, that make up the polygon. Then, subtract 3 from the number of sides. Next, multiply that number by the number of sides. Finally, divide the answer by 2, and you’ll have the number of diagonals within the polygon. For example, if a polygon has 6 sides, you’d find it has 9 diagonals. For an alternate way to determine the number of diagonals in a polygon, read on!

Did this summary help you?
Advertisement