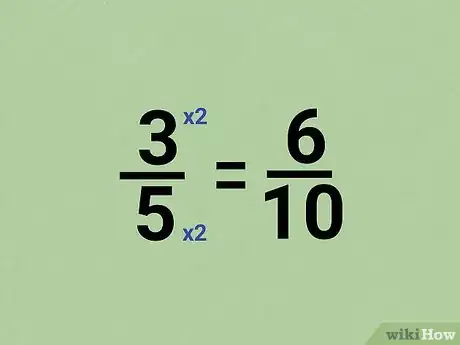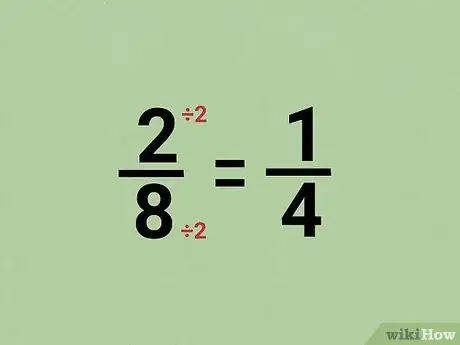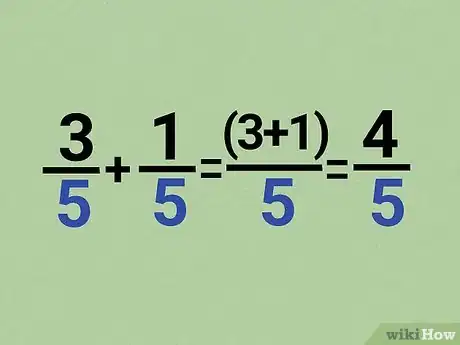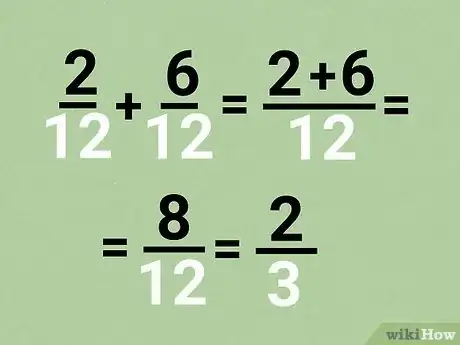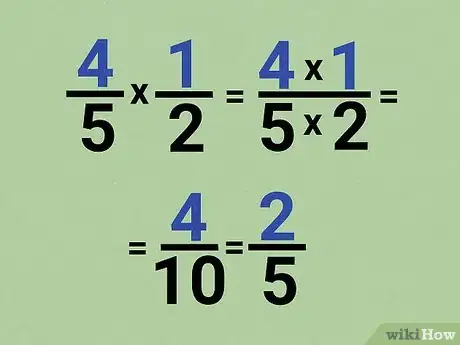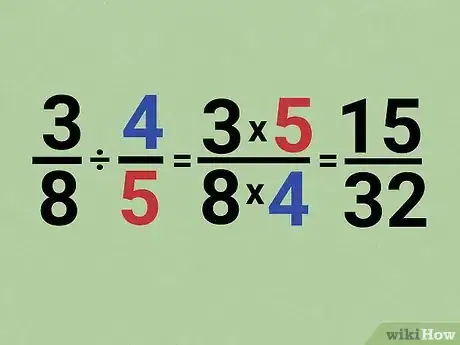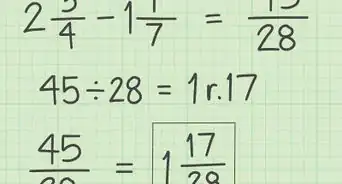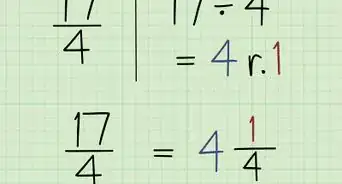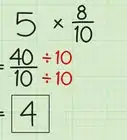This article was co-authored by David Jia and by wikiHow staff writer, Hunter Rising. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
There are 10 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 509,628 times.
Fractions represent how many parts of a whole you have, which makes them useful for taking measurements or calculating precise values. Fractions can be a difficult concept to learn since they have special terms and rules for using them in equations. Once you understand the parts of a fraction, practice doing addition and subtraction problems with them. When you know how to add and subtract fractions, you can move on to trying multiplication and division with fractions.
Steps
Understanding Fractions
-
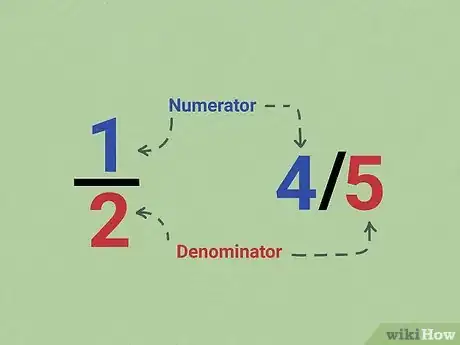
1Identify the numerator and denominator. The top number of a fraction is known as the numerator and represents how many parts of the whole you have. The bottom number of the fraction is the denominator, which is the number of parts that would equal the whole. If the numerator is smaller than the denominator, then it is a proper fraction. If the numerator was greater than the denominator, then the fraction is improper.[1]
- For example, in the fraction ½, the 1 is the numerator and 2 is the denominator.
- You can also write fractions on a single line, like 4/5. The number on the left is always the numerator and the number on the right is the denominator.
-
2Know fractions are equal if you multiply the numerator and denominator by the same number. Equivalent fractions are the same amount but written with different numerators and denominators. If you want to make a fraction that’s equivalent to the one you have, multiply the numerator and denominator by the same number and write the result as your new fraction.[2]
- For example, if you want to make an equivalent fraction to 3/5, you can multiply both numbers by 2 to make the fraction 6/10.
- In a real-world example, if you have 2 equal slices of pizza and you cut one of them in half, the two halves are still the same amount as the other full slice.
Advertisement -
3Simplify fractions by dividing the numerator and denominator by a common multiple. Many times, you’ll be asked to write a fraction in its simplest terms. If you have larger numbers in the numerator and denominator, look for a common factor that each number shares. Divide the numerator and denominator separately by the factor you found to reduce the fraction to an easier number to read.[3]
- For example, if you have the fraction 2/8, both the numerator and denominator are divisible by 2. Divide each number by 2 to get 2/8 = 1/4.
-
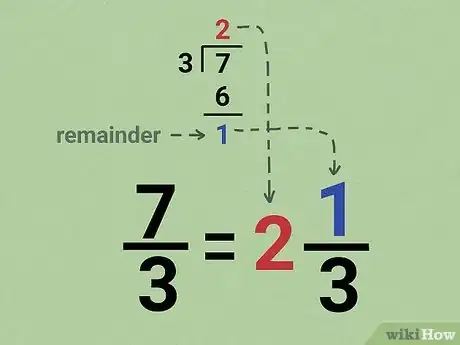
4Convert improper fractions to mixed numbers if the numerator is greater than the denominator. Improper fractions are when the numerator is larger than the denominator. To simplify an improper fraction, divide the numerator by the denominator to find a whole number and a remainder. Write the whole number first, and then make a new fraction where the numerator is the remainder you found and the denominator is the same.[4]
- For example, if you want to simplify 7/3, divide 7 by 3 to get the answer 2 with a remainder of 1. Your new mixed number will look like 2 ⅓.
Tip: If the numerator and denominator equal one another, then they can always be simplified to 1.
-
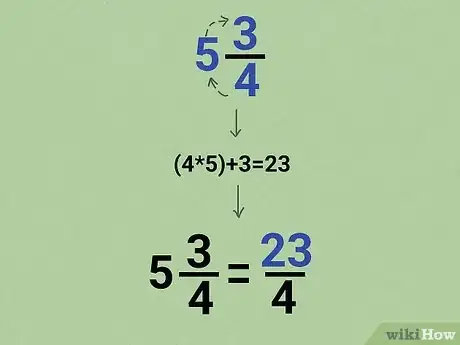
5Change mixed numbers into fractions when you need to use them in equations. When you want to use a mixed number in an equation, it’s easiest to change it back to an improper fraction so you can easily do the math. To convert the mixed number back to a fraction, multiply the whole number by the denominator. Add the result to the numerator to finish your equation.[5]
- For example, if you want to convert 5 ¾ to an improper fraction, multiply 5 x 4 = 20. Add 20 to the numerator to get the fraction 23/4.
Adding and Subtracting
-
1Add or subtract just the numerators if the denominators are the same. If the values for all the denominators in the equation are the same, only add or subtract the numerators. Rewrite the equation so the numerators are added or subtracted in parentheses over the denominator. Solve for the numerator and simplify the fraction if you’re able to.[6]
- For example, if you wanted to solve 3/5 + 1/5, rewrite the equation as (3+1)/5 = 4/5.
- If you want to solve 5/6 - 2/6, write it as (5-2)/6 = 3/6. Both the numerator and denominator are divisible by 3, so you can simplify the fraction to 1/2.
- If you have mixed numbers, remember to change them to improper fractions first. For example, if you want to solve 2 ⅓ + 1 ⅓, change the mixed numbers so the problem reads 7/3 + 4/3. Rewrite the equation like (7 + 4)/3 = 11/3. Then convert it back to a mixed number, which would be 3 ⅔.
Warning: Never add or subtract the denominators. The denominators only represent how many parts make up a whole while the numerator represents how many parts you have.
-
2Find a common multiple for the denominators if they’re different. Many times, you’ll encounter problems where the denominators are different. In order to solve the problem, the denominators need to be the same or else you’ll do your math incorrectly. List the multiples of each denominator until you find one that the numbers have in common. If you still can’t find a common multiple, then multiply the denominators together to find a common multiple.[7]
- For example, if you want to solve 1/6 + 2/4, list the multiples of 6 and 4.
- Multiples of 6: 0, 6, 12, 18…
- Multiples of 4: 0, 4, 8, 12, 16…
- The least common multiple of 6 and 4 is 12.
-
3Make equivalent fractions so the denominators are the same. Multiply the numerator and denominator of the first fraction in the equation by the multiple needed so the denominator equals the common multiple. Then do the same for the second fraction in the equation with the factor that makes its denominator is the common multiple.[8]
- In the example 1/6 + 2/4, multiply the numerator and denominator of 1/6 by 2 to get 2/12. Then multiply both numbers of 2/4 by 3 to equal 6/12.
- Rewrite the equation as 2/12 + 6/12.
-
4Solve the equation as you normally would. Once you have the denominators at the same value, add the numerators together as you normally would to get your result. If you can simplify the fraction, then reduce it to its lowest terms.[9]
- For example, rewrite 2/12 +6/12 as (2+6)/12 = 8/12.
- Simplify your answer by dividing the numerator and denominator by 4 to get a final answer of ⅔.
Multiplying and Dividing
-
1Multiply the numerators and denominators separately to find the product. When you want to multiply fractions, multiply the 2 numerators together first and write it on top. Then multiply the denominators together and write it on the bottom of the fraction. Simplify your answer if you can so it is in the lowest terms.[10]
- For example, if you want to solve 4/5 x 1/2, multiply the numerators for 4 x 1 = 4.
- Then multiply the denominators for 5 x 2 = 10.
- Write the new fraction 4/10 and simplify it by dividing the numerator and denominator by 2 to get the final answer of 2/5.
- As another example, the problem 2 ½ x 3 ½ = 5/2 x 7/2 = (5 x 7)/(2 x 2) = 35/4 = 8 ¾.
-
2Flip the numerator and denominator for the second fraction in a division problem. When you divide by a fraction, you actually use the inverse of the second number, which is also known as the reciprocal. To find the reciprocal of a fraction, simply flip the numerator and denominator to switch the numbers.[11]
- For example, the reciprocal of 3/8 is 8/3.
- Convert a mixed number into an improper fraction before taking the reciprocal. For example, 2 ⅓ converts to 7/3 and the reciprocal is 3/7.
-
3Multiply the first fraction by the second fraction’s reciprocal to find the quotient. Set up your original problem as a multiplication problem, but change the second fraction to its reciprocal. Multiply the numerators together and then multiply the denominators together to find the answer to the problem. Reduce your fraction to the simplest terms if you’re able to.[12]
- For example, if your original problem was 3/8 ÷ 4/5, first find the reciprocal of 4/5, which is 5/4.
- Rewrite your problem as multiplication with the reciprocal for 3/8 x 5/4.
- Multiply the numerators for 3 x 5 = 15.
- Multiply the denominators for 8 x 4 = 32.
- Write the new fraction 15/32.
Expert Q&A
Did you know you can get expert answers for this article?
Unlock expert answers by supporting wikiHow
-
QuestionHow do you divide fractions?
David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Math TutorWhen you're dividing fractions, flip the second fraction upside down, then multiply the tops and bottoms of the two fractions together. This is called taking the reciprocal.
Support wikiHow by unlocking this expert answer.
-
QuestionHow do you add and subtract fractions?David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Math TutorTo add and subtract fractions, you always have to find a common denominator. For example, if you need to add 1/6 and 1/2, you can't just add the tops and bottoms together. Instead, you have to find a common denominator. In this case, you can multiply the top and bottom of 1/2 by 3 to get 3/6. Then, you can add 1/6 and 3/6 to get 4/6, which you can simplify to 2/3.Support wikiHow by unlocking this expert answer.
-
QuestionWhat is a fraction?David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Math TutorFractions are a form of division—the numerator is being divided by the denominator. For example, 3/4 is the same as 3 divided by 4.Support wikiHow by unlocking this expert answer.
References
- ↑ https://www.mathsisfun.com/definitions/fraction.html
- ↑ https://www.mathsisfun.com/equivalent_fractions.html
- ↑ https://www.mathsisfun.com/simplifying-fractions.html
- ↑ https://youtu.be/nWZnyRTwBFM?t=15
- ↑ https://www.calculatorsoup.com/calculators/math/mixed-number-to-improper-fraction.php
- ↑ https://edu.gcfglobal.org/en/fractions/adding-and-subtracting-fractions/1/
- ↑ https://edu.gcfglobal.org/en/fractions/adding-and-subtracting-fractions/1/
- ↑ https://www.mathsisfun.com/equivalent_fractions.html
- ↑ https://www.bbc.co.uk/bitesize/topics/zhdwxnb/articles/z9n4k7h
About This Article
To understand a fraction, first identify the numerator and the denominator. The numerator is the number on top, which tells you how many parts of a whole the fraction represents. The denominator, which is on the bottom, represents the total number of possible parts making up the whole. For instance, the fraction ¾ describes 3 equal parts of a whole that has been divided up into 4 parts total. 3 is the numerator, while 4 is the denominator. Some fractions can be simplified, which means that you can divide the numerator and denominator by a common factor to create an equivalent fraction. For example, in the fraction 2/4, you can divide both the numerator and denominator by 2 to get the equivalent fraction ½. A fraction where the numerator is larger than the denominator is called an improper fraction. This kind of fraction represents a combination of a whole number and a fraction. You can convert improper fractions into mixed numbers by dividing the numerator by the denominator. The quotient in the division problem is the whole number, while the remainder is the numerator of the fraction. For instance, to turn 7/3 into a mixed number, divide 7 by 3 to get 2, with a remainder of 1. Write the fraction as the mixed number 2 1/3. You can add and subtract fractions like whole numbers, but only if they share the same denominator. For instance, 2/6 + 3/6 = 5/6. If the denominators are different, you’ll need to convert at least one of the fractions into an equivalent fraction so that the denominators match. Multiplying fractions is simple—just multiply the numerators by the numerators and the denominators by the denominators. To divide one fraction by another, flip the second fraction over to find its reciprocal, then multiply the two fractions together.
