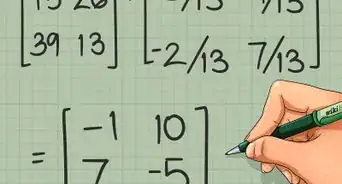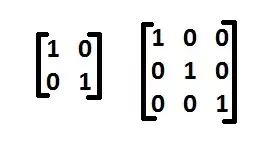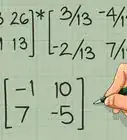Find the eigenvalues, eigenvectors, and the diagonal matrix
This article was co-authored by wikiHow staff writer, Kyle Smith. Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
This article has been viewed 1,144 times.
Learn more...
Finding a diagonal matrix can be a lengthy process, but it’s easy if you know the steps! You’ll need to calculate the eigenvalues, get the eigenvectors for those values, and use the diagonalization equation. Diagonal matrices are great for many different operations, such as computing the powers of the matrix. This wikiHow guide shows you how to diagonalize a matrix.
Things You Should Know
- Find the eigenvalues of your given matrix.
- Use the eigenvalues to get the eigenvectors.
- Apply the diagonalization equation using the eigenvectors to find the diagonal matrix.
- Note that not all matrices can be diagonalized.
Steps
Find the Eigenvalues
-
1Recall the equation for finding eigenvalues. Eigenvalues are the scalar value associated with an eigenvector, represented by the symbol lambda (λ). To find eigenvalues, use the following equation:[1]
- In other words, the determinant of lambda times the identity matrix minus the given transformation matrix.
-
2Set up the determinant equation. Here is an example for a 2 by 2 matrix:Advertisement
-
3Simplify the determinant equation. The equation simplifies to:
-
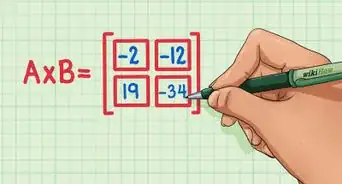
4Solve for the determinant. To do so in a 2 by 2 matrix, multiply the top-left value and the bottom-right value, then subtract the product of the top-right value and bottom-left value. We also have a guide for finding the determinant for 3x3 matrices. Continuing our example:
- and
- These two values are the eigenvalues.
Find the Eigenvectors
-
1Use the equation to find eigenvectors. Recall that the equation to find eigenvectors for a given lambda:[2]
-
- In other words, a given transformation matrix (A) times the eigenvector (V) equals the eigenvalue (lambda) times the eigenvector (V).
- This can be rewritten as:
- Where I is the identity matrix.
-
-
2Plug in an eigenvalue to the equation. For example, using the eigenvalue lambda = -5 from our problem:
-
3Find the reduced row echelon form. Use elementary row operations to get the reduced row echelon form of the new matrix. Continuing our example:
- Our starting matrix:
- The matrix in reduced row echelon form:
- Our starting matrix:
-
4Find the eigenvector. To do so:
- Our starting matrix equation:
- Writing the matrix as a linear equation:
- Write the components as an eigenvector:
- Our starting matrix equation:
-
5Repeat the above eigenvector process for any other eigenvalues. You’ll need the eigenvectors for each of the eigenvalues to diagonalize the matrix. For example, repeating the process for lambda = 10 yields the eigenvector:
Diagonalize the Matrix
-
1
-
2Write P, the matrix of eigenvectors. For our example with two eigenvectors, P would be:
- Where the first column is the eigenvector of lambda = -5, and the second column is the eigenvector for lambda = 10.
-
3Find the inverse of P. For our example, the inverse of P (P^-1) is:
- Check out our expert guide to finding the inverse of a 3x3 matrix if you need a refresher!
-
4Solve for the diagonal matrix D. Use the equation P^-1 * A * P = D to diagonalize the matrix A. Continuing our example:
- You’re done! You have diagonalized a matrix. For more linear algebra info, check out how to divide matrices and how to transpose a matrix.
References
- ↑ https://math.libretexts.org/Bookshelves/Linear_Algebra/A_First_Course_in_Linear_Algebra_(Kuttler)/07%3A_Spectral_Theory/7.01%3A_Eigenvalues_and_Eigenvectors_of_a_Matrix
- ↑ https://www.khanacademy.org/math/linear-algebra/alternate-bases/eigen-everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example
- ↑ https://www.youtube.com/watch?v=U8R54zOTVLw
- ↑ https://www.youtube.com/watch?v=PFDu9oVAE-g
- ↑ https://math.libretexts.org/Bookshelves/Linear_Algebra/A_First_Course_in_Linear_Algebra_(Kuttler)/07%3A_Spectral_Theory/7.02%3A_Diagonalization