Chapter 7
Linear Momentum and Collisions
By Boundless

Linear momentum is the product of the mass and velocity of an object, it is conserved in elastic and inelastic collisions.

In the most general form, Newton's 2nd law can be written as
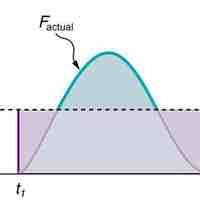
Impulse, or change in momentum, equals the average net external force multiplied by the time this force acts.
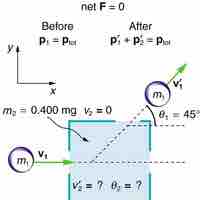
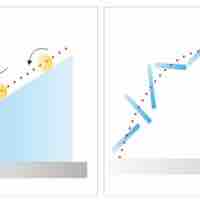
In an inelastic collision the total kinetic energy after the collision is not equal to the total kinetic energy before the collision.
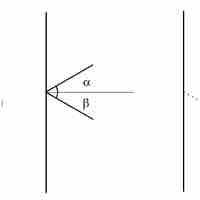
Glancing collision is a collision that takes place under a small angle, with the incident body being nearly parallel to the surface.

An elastic collision is a collision between two or more bodies in which kinetic energy is conserved.
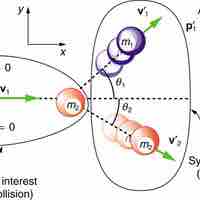
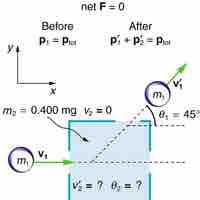
To solve a two dimensional elastic collision problem, decompose the velocity components of the masses along perpendicular axes.

Collisions may be classified as either inelastic or elastic collisions based on how energy is conserved in the collision.
While inelastic collisions may not conserve total kinetic energy, they do conserve total momentum.
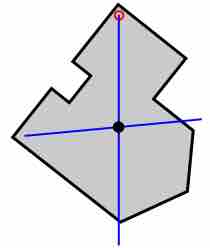
The position of COM is mass weighted average of the positions of particles. Mathematically, it is given as
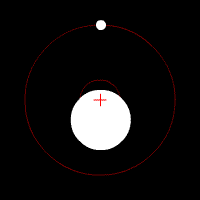
We can describe the translational motion of a rigid body as if it is a point particle with the total mass located at the COM—center of mass.

The center of mass (COM) is an important physical concept—it is the point about which objects rotate.
The COM (center of mass) of a system of particles is a geometric point that assumes all the mass and external force(s) during motion.

